搜索
【题目】求证：不论k为何值，关于x的方程 x2+（k+4）x+2k-1=0一定有两个不相等的实数根。
参考答案：
【答案】见详解
【解析】
由△=（k+4）2-4（2k-1）=k2+8k+16-8k+4=k2+20＞0，依据根的判别式即可得证．
解：∵△=（k+4）2-4（2k-1）
=k2+8k+16-8k+4
=k2+20＞0，
∴不论k为何值，关于x的方程x2+（k+4）x+2k-1=0一定有两个不相等的实数根．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知△ABC内接于⊙O，AC是⊙O的直径，D是
的中点．过点D作CB的垂线，分别交CB、CA延长线于点F、E．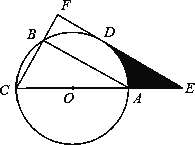 
（1）判断直线EF与⊙O的位置关系，并说明理由；
（2）若CF=6，∠ACB=60°，求阴影部分的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】某食品公司产销一种食品，已知每月的生产成本y1与产量x之间是一次函数关系，函数y1与自变量z（kg）的部分对应值如下表：
x（单位：kg）
10
20
30
y1（单位：/元）
3030
3060
3090
（1）求y1与x之间的函数关系式；
（2）经过试销发现，这种食品每月的销售收入y2（元）与销量x（kg）之间满足如图所示的函数关系
①y2与x之间的函数关系式为；
（3）②假设该公司每月生产的该种食品均能全部售出，那么该公司每月至少要生产该种食品多少kg，才不会亏损？ -
科目： 来源： 题型：
查看答案和解析>>【题目】先化简，再求值：
（1）
m﹣（
m﹣1）+3（4﹣m），其中m是最大的负整数．
（2）7a2b+（﹣4a2b+5c）﹣2（2a2b+3c），其中ab=1，a+c=5． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知直线l1：y=x+3与x轴交于点A，与y轴交于点B，与直线l2：y=﹣
x交于点P．直线l3：y=﹣ 
x+4与x轴交于点C，与y轴交于点D，与直线l1交于点Q，与直线l2交于点R． 
（1）点A的坐标是 ， 点B的坐标是 ， 点P的坐标是；
（2）将△POB沿y轴折叠后，点P的对应点为P′，试判断点P′是否在直线l3上，并说明理由；
（3）求△PQR的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】为了解中考体育科目训练情况，山东省阳信县从全县九年级学生中随机抽取了部分学生进行了一次中考体育科目测试（把测试结果分为四个等级：A级：优秀；B级：良好；C级：及格；D级：不及格），并将测试结果绘成了如下两幅不完整的统计图．请根据统计图中的信息解答下列问题：
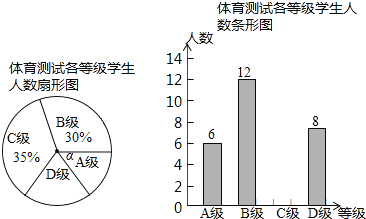
（1）本次抽样测试的学生人数是 ______ ；
（2）图1中∠α的度数是 ______ ，并把图2条形统计图补充完整；
（3）该县九年级有学生4500名，如果全部参加这次中考体育科目测试，请估计不及格的人数为 ______ ．
（4）测试老师想从4位同学（分别记为E、F、G、H，其中E为小明）中随机选择两位同学了解平时训练情况，请用列表或画树形图的方法求出选中小明的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】由于雾霾天气频发，市场上防护口罩出现热销，某医药公司每月固定生产甲、乙两种型号的防雾霾口罩共20万只，且所有产品当月全部售出，原料成本、销售单价及工人生产提成如表：
甲
乙
原料成本
12
8
销售单价
18
12
生产提成
1
0.8
（1）若该公司五月份的销售收入为300万元，求甲、乙两种型号的产品分别是多少万只？
（2）公司实行计件工资制，即工人每生产一只口罩获得一定金额的提成，如果公司六月份投入总成本（原料总成本+生产提成总额）不超过239万元，应怎样安排甲、乙两种型号的产量，可使该月公司所获利润最大？并求出最大利润（利润=销售收入﹣投入总成本）
相关试题
