【题目】已知某品牌的饮料有大瓶与小瓶装之分.某超市花了2100元购进一批该品牌的饮料共800瓶,其中,大瓶和小瓶饮料的进价及售价如右表所示.
大瓶 | 小瓶 | |
进价(元/瓶) |
|
|
售价(元/瓶) |
|
|
(1)问:该超市购进大瓶和小瓶饮料各多少瓶?
(2)当大瓶饮料售出了200瓶,小瓶饮料售出了100瓶后,商家决定将剩下的小瓶饮料的售价降低0.5元销售,并把其中一定数量的小瓶饮料作为赠品,在顾客一次性购买大瓶饮料时,每满2瓶就送1瓶小瓶饮料,送完即止.请问:超市要使这批饮料售完后获得的利润为1075元,那么小瓶饮料作为赠品送出多少瓶?
参考答案:
【答案】(1)该超市购进大瓶饮料![]() 瓶,小瓶饮料
瓶,小瓶饮料![]() 瓶;(2)小瓶饮料作为赠品送出
瓶;(2)小瓶饮料作为赠品送出![]() 瓶.
瓶.
【解析】
(1)设该超市购进大瓶饮料x瓶,小瓶饮料y瓶,根据:“该品牌的饮料共800瓶、购进大、小瓶饮料共花费2100元”列不等式组求解可得;
(2)根据:大瓶饮料的销售额+前100瓶小瓶饮料销售额+未赠送小瓶饮料销售额-总成本=1075,求解可得
(1)设该超市购进大瓶饮料![]() 瓶,小瓶饮料
瓶,小瓶饮料![]() 瓶.
瓶.
由题意得![]() ,解得
,解得![]()
答:该超市购进大瓶饮料![]() 瓶,小瓶饮料
瓶,小瓶饮料![]() 瓶.
瓶.
(2)![]()
答:小瓶饮料作为赠品送出![]() 瓶.
瓶.
-
科目: 来源: 题型:
查看答案和解析>>【题目】[问题]如图①,点
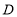 是
是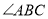 的角平分线
的角平分线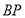 上一点,连接
上一点,连接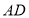 ,
,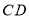 ,若
,若 与
与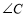 互补,则线段
互补,则线段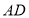 与
与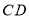 有什么数量关系?
有什么数量关系?[探究]
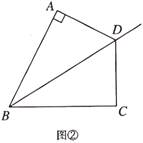
探究一:如图②,若
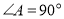 ,则
,则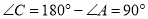 ,即
,即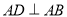 ,
,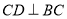 ,又因为
,又因为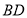 平分
平分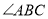 ,所以
,所以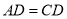 ,理由是:_______.
,理由是:_______.探究二:若
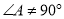 ,请借助图①,探究
,请借助图①,探究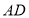 与
与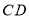 的数量关系并说明理由.
的数量关系并说明理由.[结论]点
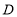 是
是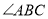 的角平分线
的角平分线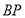 上一点,连接
上一点,连接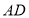 ,
,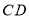 ,若
,若 与
与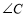 互补,则线段
互补,则线段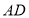 与
与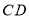 的数量关系是______.
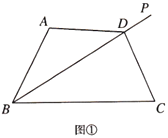
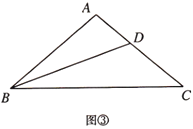
的数量关系是______.[拓展]已知:如图③,在
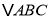 中,
中, ,
,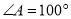 ,
,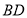 平分
平分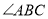 .求证:
.求证: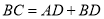 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=ax+b(a、b是常数,a≠0)函数图象经过(﹣1,4),(2,﹣2)两点,下面说法中:(1)a=2,b=2;(2)函数图象经过(1,0);(3)不等式ax+b>0的解集是x<1;(4)不等式ax+b<0的解集是x<1;正确的说法有____________________.(请写出所有正确说法的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:在
 中,
中, ,
, .
.(1)按下列步骤用尺规作图(保留作图痕迹,不写出作法):作
 的平分线AD,交BC于D;
的平分线AD,交BC于D;(2)在(1)中,过点D作
 ,交AB于点E,若CD=4,则BC的长为 .
,交AB于点E,若CD=4,则BC的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,抛物线y= x2+bx+c与x轴、y轴分别相交于点A( 1,0)、B(0,3)两点,其顶点为D.
(1)求这条抛物线的解析式;
(2)若抛物线与x轴的另一个交点为E. 求△ODE的面积;抛物线的对称轴上是否存在点P使得△PAB的周长最短。若存在请求出P点的坐标,若不存在说明理由。

相关试题

