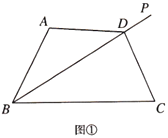
【题目】[问题]如图①,点![]() 是
是![]() 的角平分线
的角平分线![]() 上一点,连接
上一点,连接![]() ,
,![]() ,若
,若![]() 与
与![]() 互补,则线段
互补,则线段![]() 与
与![]() 有什么数量关系?
有什么数量关系?
[探究]
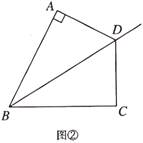
探究一:如图②,若![]() ,则
,则![]() ,即
,即![]() ,
,![]() ,又因为
,又因为![]() 平分
平分![]() ,所以
,所以![]() ,理由是:_______.
,理由是:_______.
探究二:若![]() ,请借助图①,探究
,请借助图①,探究![]() 与
与![]() 的数量关系并说明理由.
的数量关系并说明理由.
[结论]点![]() 是
是![]() 的角平分线
的角平分线![]() 上一点,连接
上一点,连接![]() ,
,![]() ,若
,若![]() 与
与![]() 互补,则线段
互补,则线段![]() 与
与![]() 的数量关系是______.
的数量关系是______.
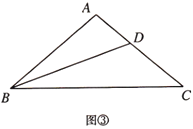
[拓展]已知:如图③,在![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() .求证:
.求证:![]() .
.
参考答案:
【答案】探究一:角的平分线上的点到角的两边距离相等;探究二:AD=CD;理由见解析;[结论]:AD=CD;[拓展]:见解析.
【解析】
探究一:根据角平分线的性质定理解答;
探究二:作![]() 于
于![]() ,作
,作![]() 交
交![]() 的延长线于
的延长线于![]() ,证明
,证明![]() ,根据全等三角形的性质证明结论;
,根据全等三角形的性质证明结论;
[理论] 根据探究结果得到答案;
[拓展]在![]() 上取一点
上取一点![]() ,使
,使![]() ,作
,作![]() 角
角![]() 的延长线于
的延长线于![]() ,
,![]() 于
于![]() ,证明
,证明![]() ,得到
,得到![]() ,根据等腰三角形的性质得到
,根据等腰三角形的性质得到![]() ,等量代换得到
,等量代换得到![]() ,结合图形证明结论.
,结合图形证明结论.
解:探究一:![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
理由是:角平分线上的点到角的两边的距离相等,
故答案为:角平分线上的点到角的两边的距离相等;
探究二:作![]() 于
于![]() ,作
,作![]() 交
交![]() 的延长线于
的延长线于![]() ,
,
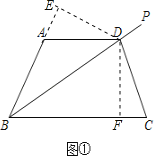
![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
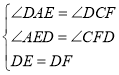 ,
,
![]()
![]() ;
;
[理论] 综上所述,点![]() 是
是![]() 的角平分线
的角平分线![]() 上一点,连接
上一点,连接![]() ,
,![]() ,若
,若![]() 与
与![]() 互补,则线段
互补,则线段![]() 与
与![]() 的数量关系是
的数量关系是![]() ,
,
故答案为:![]() ;
;
[拓展] 在![]() 上取一点
上取一点![]() ,使
,使![]() ,作
,作![]() 角
角![]() 的延长线于
的延长线于![]() ,
,![]() 于
于![]() ,
,
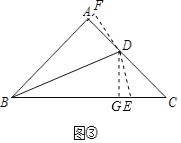
![]() .
.
![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,
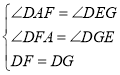 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人分别骑自行车和摩托车,从同一地点沿相同的路线前往距离80km的某地,图中l1,l2分别表示甲、乙两人离开出发地的距离s(km)与行驶时间t(h)之间的函数关系.请根据图象解答下列问题:
(1)甲、乙两人谁到达目的地较早?早多长时间?
(2)分别求甲、乙两人行驶过程中s与t的函数关系式;
(3)试确定当两辆车都在行驶途中(不包括出发地和目的地)时,t的取值范围;并在这一时间段内,求t为何值时,摩托车行驶在自行车前面?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场购进一批日用品,若按每件5元的价格销售,每月能卖出3万件;若按每件6元的价格销售,每月能卖出2万件,假定每月销售件数
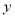 (件)与价格
(件)与价格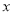 (元/件)之间满足一次函数关系.
(元/件)之间满足一次函数关系.(1)试求:y与x之间的函数关系式;
(2)这批日用品购进时进价为4元,则当销售价格定为多少时,才能使每月的润最大?每月的最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分为100分).
他们的各项成绩如下表所示:
修造人
笔试成绩/分
面试成绩/分
甲
90
88
乙
84
92
丙
x
90
丁
88
86
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=ax+b(a、b是常数,a≠0)函数图象经过(﹣1,4),(2,﹣2)两点,下面说法中:(1)a=2,b=2;(2)函数图象经过(1,0);(3)不等式ax+b>0的解集是x<1;(4)不等式ax+b<0的解集是x<1;正确的说法有____________________.(请写出所有正确说法的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某品牌的饮料有大瓶与小瓶装之分.某超市花了2100元购进一批该品牌的饮料共800瓶,其中,大瓶和小瓶饮料的进价及售价如右表所示.
大瓶
小瓶
进价(元/瓶)


售价(元/瓶)


(1)问:该超市购进大瓶和小瓶饮料各多少瓶?
(2)当大瓶饮料售出了200瓶,小瓶饮料售出了100瓶后,商家决定将剩下的小瓶饮料的售价降低0.5元销售,并把其中一定数量的小瓶饮料作为赠品,在顾客一次性购买大瓶饮料时,每满2瓶就送1瓶小瓶饮料,送完即止.请问:超市要使这批饮料售完后获得的利润为1075元,那么小瓶饮料作为赠品送出多少瓶?
相关试题

