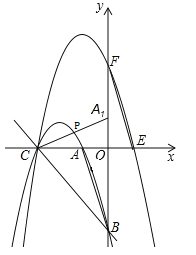
【题目】如图1,在平面直角坐标系![]() 中,已知点
中,已知点![]() 和点
和点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 按顺时针分别旋转
按顺时针分别旋转![]() ,
,![]() 得到
得到![]() ,
,![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,
,![]() ,
,![]() ;抛物线
;抛物线![]() 经过点
经过点![]() ,
,![]() ,
,![]() .
.

(1)点![]() 的坐标为________,点
的坐标为________,点![]() 的坐标为________;抛物线
的坐标为________;抛物线![]() 的解析式为________,抛物线
的解析式为________,抛物线![]() 的解析式为________;
的解析式为________;
(2)如果点![]() 是直线
是直线![]() 上方抛物线
上方抛物线![]() 上的一个动点.
上的一个动点.
①若![]() ,求
,求![]() 点的坐标;
点的坐标;
②如图2,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,交抛物线
,交抛物线![]() 于点
于点![]() ,记
,记![]() ,求
,求![]() 与
与![]() 的函数关系式.当
的函数关系式.当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ,
,![]() ,
,![]() :
:![]() ,
,![]() :
:![]() .(2)①符合条件的点
.(2)①符合条件的点![]() 的坐标为
的坐标为![]() 或
或![]() .②
.②![]() .
.
【解析】
(1)根据旋转的性质,可得C,E,F的坐标,根据待定系数法求解析式;
(2)①根据P点关于直线CA或关于x轴对称直线与抛物线交点坐标,求出解析式,联立方程组求解;
②根据图象上的点满足函数解析式,可得P、N、M纵坐标,根据平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得二次函数,根据x取值范围讨论h范围.
(1)由旋转可知,OC=6,OE=2,
则点C坐标为(-6,0),E点坐标为(2,0),
分别利用待定系数法求C1解析式为:y=-![]() x24x6,C2解析式为:y=-
x24x6,C2解析式为:y=-![]() x22x+6
x22x+6
(2)①若点P在x轴上方,∠PCA=∠ABO时,则CA1与抛物线C1的交点即为点P,如图,
设直线CA1的解析式为:y=k1x+b1
∴![]()
解得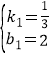
∴直线CA1的解析式为:y=![]() x+2
x+2
联立: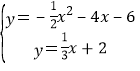 ,解得
,解得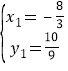 或
或![]() (舍去),
(舍去),
∴P(![]() )
)
若点P在x轴下方,∠PCA=∠ABO时,则CH与抛物线C1的交点即为点P,如图,
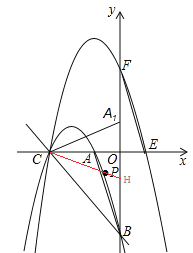
易知OH=OA,
∴H(0,-2)
设直线CH的解析式为:y=k2x+b2
∴![]()
解得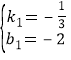
∴直线CH的解析式为:y=![]() x-2
x-2
联立: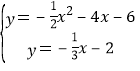 ,解得
,解得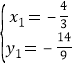 或
或![]() (舍去),
(舍去),
∴![]() ;
;
∴符合条件的点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
②设直线![]() 的解析式为:
的解析式为:![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴直线![]() 的解析式为:
的解析式为:![]() ,
,
过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() ,
,

设P(x,-![]() x24x6)
x24x6)
∴![]() ,
,
![]()
![]()
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
当![]() 时,
时,![]() 的最大值为21.
的最大值为21.
∵![]() ,当
,当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
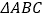 中,
中,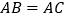 ,以
,以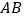 为直径的
为直径的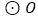 交
交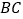 于点
于点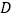 ,交
,交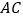 于点
于点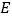 ,过点
,过点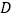 作
作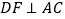 于点
于点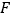 ,交
,交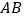 的延长线于点
的延长线于点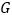 .
.
(1)求证:
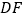 是
是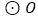 的切线;
的切线;(2)已知
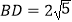 ,
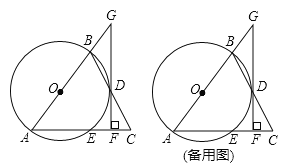
,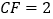 ,求
,求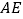 和
和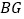 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC,AB=AC,AC的垂直平分线与AB所在直线相交所得的锐角为40°,∠C=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市盘山、黄崖关长城、航母公园三景区是人们节假日游玩的热点景区.某中学对七年级(1)班学生今年暑假到这三景区游玩的计划做了全面调查,调查分四个类别,A游三个景区;B:游两个景区;C:游一个景区;D:不到这三个景区游玩.根据调查的结果绘制了不完全的条形统计图和扇形统计图(如图①、图②)如下,请根据图中所给的信息,解答下列问题:
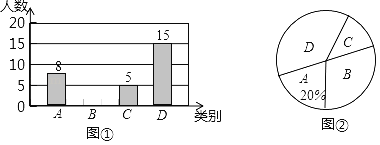
(1)求七年级(1)班学生人数;
(2)将条形统计图补充完整;
(3)求扇形统计图中表示“B类别”的圆心角的度数;
(4)若该中学七年级有学生520人,求计划暑假选择A、B、C三个类别出去游玩的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电器超市销售每台进价分别为160元、120元的A、B两种型号的电风扇,如表是近两周的销售情况:(进价、售价均保持不变,利润=销售收入﹣进货成本)
销售时段
销售数量
销售收入
A种型号
种型号
第一周
3台
4台
1200元
第二周
5台
6台
1900元
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠A=∠AGE,∠D=∠DGC.
(1)试说明AB∥CD;
(2)若∠1+∠2=180°,且∠BEC=2∠B+60°,求∠C的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A、B在坐标轴上,其中A(0,
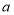 )、B(
)、B(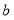 ,0)满足:
,0)满足: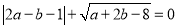
(1)求A、B两点的坐标;
(2)将线段AB平移到CD,点A的对应点为C(-2,t),如图(1)所示.若三角形ABC的面积为9,求点D的坐标.
相关试题

