【题目】用电脑程序控制小型赛车进行比赛,“复兴号”和“和谐号”两辆赛车进入了决赛.两辆赛车从距离终点75米的某地同时出发,“复兴号”比“和谐号”早t秒到达终点,且“复兴号”的平均速度是“和谐号”的m倍.
(1)当m=1.2,t=5时,求“复兴号”的平均速度是多少米/秒?
(2)“和谐号”的平均速度为 米/秒(用含m、t的式子表示).
参考答案:
【答案】(1) “复兴号”的平均速度是3米/秒.(2)![]() .
.
【解析】
(1)根据“和谐号所用时间-复兴号所用时间=复兴号”比“和谐号”早到的时间”这一等量关系,列出方程解之即可.
(2)根据“和谐号所用时间-复兴号所用时间=复兴号”比“和谐号”早到的时间”等量关系,用含m、t的式子将“和谐号”的平均速度表示出来即可.
(1)解:设“和谐号”的平均速度为x米/秒,则“复兴号”的平均速度为1.2x米/秒,根据题意得:
![]()
解得:x=2.5
检验:当x=2.5时,1.2x≠0,故x=2.5是方程的解
所以“复兴号”的平均速度是1.2×2.5=3米/秒
答:“复兴号”的平均速度是3米/秒.
(2)解:设“和谐号”的平均速度为x米/秒,则“复兴号”的平均速度为mx米/秒,
根据题意得:
![]()
解得:![]()
经检验:当![]() 时,mx≠0,故
时,mx≠0,故![]() 是方程的解
是方程的解
答:“和谐号”的平均速度为![]() 米/秒
米/秒
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,四边形ABCD的顶点A在
,四边形ABCD的顶点A在 的内部,B,C两点在OM上(C在B,O之间),且
的内部,B,C两点在OM上(C在B,O之间),且 ,点D在ON上,若当CD⊥OM时,四边形ABCD的周长最小,则此时AD的长度是__________.
,点D在ON上,若当CD⊥OM时,四边形ABCD的周长最小,则此时AD的长度是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的顶点A在y轴的正半轴上,点C在x轴的正半轴上,反比例函数y=
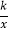 (k≠0)的图象的一个分支与AB交于点D,与BC交于点E,DF⊥x轴于点F,EG⊥y轴于点G,交DF于点H.若矩形OGHF和矩形HDBE的面积分别是2和5,则k的值是( )
(k≠0)的图象的一个分支与AB交于点D,与BC交于点E,DF⊥x轴于点F,EG⊥y轴于点G,交DF于点H.若矩形OGHF和矩形HDBE的面积分别是2和5,则k的值是( )
A. 7 B.
 C. 2+
C. 2+ D. 10
D. 10 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A(2,3)和点B(0,2),点A在反比例函数y=
 的图象上,作射线AB,交反比例函数图象于另一点M,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则CM的长度为( )
的图象上,作射线AB,交反比例函数图象于另一点M,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则CM的长度为( )
A. 5 B. 6 C. 4
 D. 5
D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC是等边三角形,点D在BC边上,点E在AB的延长线上,将DE绕D点顺时针旋转120°得到DF.

(1)如图1,若点F恰好落在AC边上,求证:点D是BC的中点;
(2)如图2,在(1)的条件下,若
 =45°,连接AD,求证:
=45°,连接AD,求证: ;
;(3)如图3,若
 ,连CF,当CF取最小值时,直接写出
,连CF,当CF取最小值时,直接写出 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知点
 ,
, 与坐标原点O在同一直线上,且AO=BO,其中m,n满足
与坐标原点O在同一直线上,且AO=BO,其中m,n满足 .
.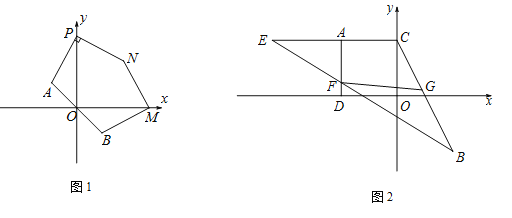
(1)求点A,B的坐标;
(2)如图1,若点M,P分别是x轴正半轴和y轴正半轴上的点,点P的纵坐标不等于2,点N在第一象限内,且
 ,PA⊥PN,
,PA⊥PN, ,求证:BM⊥MN;
,求证:BM⊥MN;(3)如图2,作AC⊥y轴于点C,AD⊥x轴于点D,在CA延长线上取一点E,使
 ,连结BE交AD于点F,恰好有
,连结BE交AD于点F,恰好有 ,点G是CB上一点,且
,点G是CB上一点,且 ,连结FG,求证:
,连结FG,求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点为 A(2,2),B(5,3),C(3,5).

(1)请作出△ABC关于y轴的对称图形△A1B1C1,并写出点A的对称点A1的坐标;
(2)点M是第一象限内一点(不与点A重合),且M点的横、纵坐标都为整数.
①若
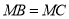 ,请直接写出一个满足条件的M点的坐标;
,请直接写出一个满足条件的M点的坐标;②若
 ,请直接写出一个满足条件的M点的坐标;
,请直接写出一个满足条件的M点的坐标;(3)将△A1B1C1向右平移n个单位长度得到△A2B2C2,若△ABC与△A2B2C2关于某条直线l对称,则直线l与x轴交点的横坐标为 (用含n的式子表示).
相关试题

