【题目】如图1,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.
(1)当t=![]() 时,则OP= ,S△ABP= ;
时,则OP= ,S△ABP= ;
(2)当△ABP是直角三角形时,求t的值;
(3)如图2,当AP=AB时,过点A作AQ∥BP,并使得∠QOP=∠B,求证:AQ·BP=3.

参考答案:
【答案】(1)1, ![]() ;(2)1或
;(2)1或![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】试题分析:(1)如答图1所示,作辅助线,利用三角函数或勾股定理求解;
(2)当△ABP是直角三角形时,有三种情形,需要分类讨论;
(3)如答图4所示,作辅助线,构造一对相似三角形△OAQ∽△PBO,利用相似关系证明结论.
试题解析:(1)1, ![]()

(2)①∵∠A<∠BOC=60,∴∠A不可能是直角
②当∠ABP=90时
∵∠BOC=60,∴∠OPB=30
∴OP=2OB,即2t=2
∴t=1
③当∠APB=90时
作PD⊥AB,垂足为D,则∠ADP=∠PDB=90

∵OP=2t,∴OD=t,PD=![]() t,AD=2+t,BD=1-t(△BOP是锐角三角形)
t,AD=2+t,BD=1-t(△BOP是锐角三角形)
∴AP 2=( 2+t )2+3t 2,BP 2=( 1-t )2+3t 2
∵AP 2+BP 2=AB 2,∴( 2+t )2+3t 2+( 1-t )2+3t 2=9
即4t 2+t-2=0,解得t1
解得t1=![]() ,t2=
,t2=![]() (舍去)
(舍去)
综上,当△ABP是直角三角形时,t=1或 ![]()
(3)

连接PQ,设AP与OQ相交于点E
∵AQ∥BP,∴∠QAP=∠APB
∵AP=AB,∴∠APB=∠B
∴∠QAP=∠B
又∵∠QOP=∠B,∴∠QAP=∠QOP
∵∠QEA=∠PEO,∴△QEA∽△PEO
∴![]()
又∵∠PEQ=∠OEA,∴△PEQ∽△OEA
∴∠APQ=∠AOQ
∵∠AOC=∠AOQ+∠QOP=∠B+∠BPO
∴∠AOQ=∠BPO,
∴∠APQ=∠BPO
∴△APQ∽△BPO,
∴![]()
∴AQ·BP=AP·BO=3×1=3
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究规律:如图,已知直线m∥n,A、B为直线n上的两点,C、P为直线m上的两点.
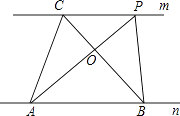
(1)请写出图中面积相等的各对三角形: .
(2)如果A、B、C为三个定点,点P在m上移动,那么无论P点移动到任何位置总有:与△ABC的面积相等;理由是: . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,M,N分别是边AB,BC的中点,MP⊥AB交边CD于点P,连接NM,NP.
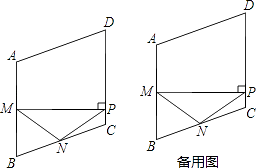
(1)若∠B=60°,这时点P与点C重合,则∠NMP=度;
(2)求证:NM=NP;
(3)当△NPC为等腰三角形时,求∠B的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,∠A:∠B:∠C:∠D的值可能是( )
A. 3:4:3:4 B. 5:2:2:5 C. 2:3:4:5 D. 3:3:4:4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是一个平行四边形,BE⊥CD于点E,BF⊥AD于点F,
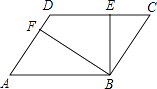
(1)请用图中表示的字母表示出平行线AD与BC之间的距离;
(2)若BE=2cm,BF=4cm,求平行线AB与CD之间的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】当x=1,y=﹣2时,代数式2x+y﹣1的值是( )
A.1
B.﹣2
C.2
D.﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,AB,BC,CD的长度分别为2x+1,3x,x+4,则ABCD的周长是_______.
相关试题

