【题目】探究规律:如图,已知直线m∥n,A、B为直线n上的两点,C、P为直线m上的两点. 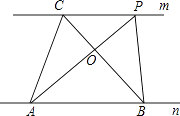
(1)请写出图中面积相等的各对三角形: .
(2)如果A、B、C为三个定点,点P在m上移动,那么无论P点移动到任何位置总有:与△ABC的面积相等;理由是: .
参考答案:
【答案】
(1)△ABC与△ABP,△CPA与△CPB
(2)△ABP;等底等高的三角形的面积相等
【解析】解:(1)请写出图中面积相等的各对三角形:△ABC与△ABP,△CPA与△CPB;(2)如果A、B、C为三个定点,点P在m上移动,那么无论P点移动到任何位置总有:△ABP与△ABC的面积相等;理由是:等底等高的三角形的面积相等, 所以答案是:△ABC与△ABP,△CPA与△CPB;△ABP,等底等高的三角形的面积相等.
【考点精析】利用平行线之间的距离和三角形的面积对题目进行判断即可得到答案,需要熟知两条平行线的距离:两条直线平行,从一条直线上的任意一点向另一条直线引垂线,垂线段的长度,叫做两条平行线的距离;三角形的面积=1/2×底×高.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在1,-1,-2这三个数中,任意两数之和的最大值是( ).
A. 1 B. 0 C. -1 D. -3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=﹣1是一元二次方程ax2+bx﹣2=0的一个根,那么b﹣a的值等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在解答“分解因式:(1)3x2-9x+3;(2)4x2-9.”时,是这样做的:
解:(1)3x2-9x+3=3(x2-6x+1);
(2)4x2-9=(2x+3)(2x-3).
请你利用分解因式与整式乘法的关系,判断他分解得对不对.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某新建火车站站前广场需要绿化的面积为46000米2,施工队在绿化了22000米2后,将每天的工作量增加为原来的1.5倍,结果提前4天完成了该项绿化工程.
(1)该项绿化工程原计划每天完成多少米2?
(2)该项绿化工程中有一块长为20米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56米2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),问人行通道的宽度是多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数
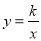 的图象上,过点A的直线y=x+b交x轴于点B.
的图象上,过点A的直线y=x+b交x轴于点B.(1)求k和b的值;
(2)求△OAB的面积.
(3)请根据图象直接写出当x取何值时 ,一次函数值大于反比例函数值。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,DE⊥AB,DF⊥AC,AE=AF,则下列结论成立的是( )
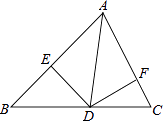
A.BD=CD
B.DE=DF
C.∠B=∠C
D.AB=AC
相关试题

