【题目】如图,四边形ABCD是一个平行四边形,BE⊥CD于点E,BF⊥AD于点F, 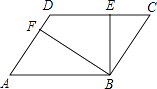
(1)请用图中表示的字母表示出平行线AD与BC之间的距离;
(2)若BE=2cm,BF=4cm,求平行线AB与CD之间的距离.
参考答案:
【答案】
(1)解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∵BF⊥AD,
∴BF⊥BC,
∴平行线AD与BC之间的距离是线段BF的长度
(2)解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∵BE⊥CD,
∴BE⊥AB,
∴平行线AD与BC之间的距离是线段BE的长度,是2cm
【解析】(1)根据平行四边形性质得出AD∥BC,求出BF⊥BC,即可得出答案;(2)根据平行四边形性质得出CD∥AB,求出BE⊥AB,即可得出答案.
【考点精析】掌握平行线之间的距离和平行四边形的性质是解答本题的根本,需要知道两条平行线的距离:两条直线平行,从一条直线上的任意一点向另一条直线引垂线,垂线段的长度,叫做两条平行线的距离;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,M,N分别是边AB,BC的中点,MP⊥AB交边CD于点P,连接NM,NP.
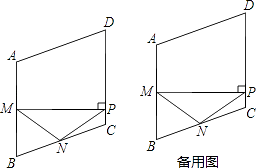
(1)若∠B=60°,这时点P与点C重合,则∠NMP=度;
(2)求证:NM=NP;
(3)当△NPC为等腰三角形时,求∠B的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,∠A:∠B:∠C:∠D的值可能是( )
A. 3:4:3:4 B. 5:2:2:5 C. 2:3:4:5 D. 3:3:4:4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.
(1)当t=
 时,则OP= ,S△ABP= ;
时,则OP= ,S△ABP= ;(2)当△ABP是直角三角形时,求t的值;
(3)如图2,当AP=AB时,过点A作AQ∥BP,并使得∠QOP=∠B,求证:AQ·BP=3.

-
科目: 来源: 题型:
查看答案和解析>>【题目】当x=1,y=﹣2时,代数式2x+y﹣1的值是( )
A.1
B.﹣2
C.2
D.﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,AB,BC,CD的长度分别为2x+1,3x,x+4,则ABCD的周长是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】省政府提出2016年要实现180 000农村贫困人口脱贫,数据180 000用科学记数法表示为( )
A.1.8×103
B.1.8×104
C.1.8×105
D.1.8×106
相关试题

