【题目】如图,已知反比例函数 ![]() 的图象经过第二象限内的点A(﹣1,m),AB⊥x轴于点B,△AOB的面积为2.若直线y=ax+b经过点A,并且经过反比例函数
的图象经过第二象限内的点A(﹣1,m),AB⊥x轴于点B,△AOB的面积为2.若直线y=ax+b经过点A,并且经过反比例函数 ![]() 的图象上另一点C(n,一2).
的图象上另一点C(n,一2).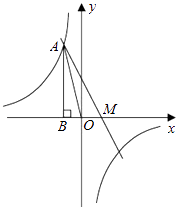
(1)求直线y=ax+b的解析式;
(2)设直线y=ax+b与x轴交于点M,求AM的长.
参考答案:
【答案】
(1)
解:∵点A(﹣1,m)在第二象限内,
∴AB=m,OB=1,
∴S△ABO= ![]() ABBO=2,
ABBO=2,
即: ![]() ×m×1=2,
×m×1=2,
解得m=4,
∴A (﹣1,4),
∵点A (﹣1,4),在反比例函数 ![]() 的图象上,
的图象上,
∴4= ![]() ,
,
解得k=﹣4,
∴反比例函数为y=﹣ ![]() ,
,
又∵反比例函数y=﹣ ![]() 的图象经过C(n,﹣2)
的图象经过C(n,﹣2)
∴﹣2= ![]() ,
,
解得n=2,
∴C (2,﹣2),
∵直线y=ax+b过点A (﹣1,4),C (2,﹣2)
∴ ![]() ,
,
解方程组得 ![]() ,
,
∴直线y=ax+b的解析式为y=﹣2x+2
(2)
解:当y=0时,即﹣2x+2=0,
解得x=1,
∴点M的坐标是M(1,0),
在Rt△ABM中,
∵AB=4,BM=BO+OM=1+1=2,
由勾股定理得AM= ![]() =
= ![]() =
= ![]()
【解析】(1)根据点A的横坐标与△AOB的面积求出AB的长度,从而得到点A的坐标,然后利用待定系数法求出反比例函数解析式,再利用反比例函数解析式求出点C的坐标,根据点A与点C的坐标利用待定系数法即可求出直线y=ax+b的解析式;(2)根据直线y=ax+b的解析式,取y=0,求出对应的x的值,得到点M的坐标,然后求出BM的长度,在△ABM中利用勾股定理即可求出AM的长度.
【考点精析】认真审题,首先需要了解一次函数的性质(一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小),还要掌握一次函数的图象和性质(一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC是直角三角形,∠A=90°,D是斜边BC的中点,E、F分别是AB、AC边上的动点,且DE⊥DF.
(1)如图1,AB=AC,BE=12,CF=5,求线段EF的长.
(2)如图2,若AB≠AC,写出线段EF与线段BE、CF之间的等量关系,并写出证明过程.

-
科目: 来源: 题型:
查看答案和解析>>【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售? -
科目: 来源: 题型:
查看答案和解析>>【题目】一位同学拿了两块45°的三角尺△MNK,△ACB做了一个探究活动:将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=a.
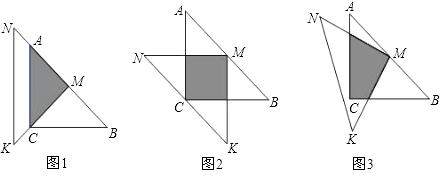
(1)如图1,两个三角尺的重叠部分为△ACM,则重叠部分的面积为 , 周长为;
(2)将图1中的△MNK绕顶点M逆时针旋转45°,得到图2,此时重叠部分的面积为 , 周长为;
(3)如果将△MNK绕M旋转到不同于图1,图2的位置,如图3所示,猜想此时重叠部分的面积为多少?并试着加以验证. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,正确的有( )
①Rt△ABC中,已知两边长分别为3和4,则第三边长为5;
②有一个内角等于其他两个内角和的三角形是直角三角形;
③三角形的三边分别为a,b,C,若a2+c2=b2,那么∠C=90°;
④若△ABC中,∠A:∠B:∠C=1:5:6,则△ABC是直角三角形.
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D交AC于点E,那么下列结论中正确的是 ( )
①△BDF和△CEF都是等腰三角形
②DE=BD+CE
③△ADE的周长等于AB和AC的和
④BF=CF

A. ①②③④ B. ①②③ C. ①② D. ①
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=ax2﹣2ax﹣1(a是常数,a≠0),下列结论正确的是( )
A.当a=1时,函数图象过点(﹣1,1)
B.当a=﹣2时,函数图象与x轴没有交点
C.若a>0,则当x≥1时,y随x的增大而减小
D.若a<0,则当x≤1时,y随x的增大而增大
相关试题

