【题目】如图所示,△ABC是直角三角形,∠A=90°,D是斜边BC的中点,E、F分别是AB、AC边上的动点,且DE⊥DF.
(1)如图1,AB=AC,BE=12,CF=5,求线段EF的长.
(2)如图2,若AB≠AC,写出线段EF与线段BE、CF之间的等量关系,并写出证明过程.

参考答案:
【答案】(1)13;(2)EF2=BE2+CF2,证明见解析.
【解析】
(1)首先连接AD,由△ABC是等腰直角三角形,AB=AC,AD是斜边的中线,可得:AD=DC,∠EAD=∠C=45°,AD⊥BC即∠CDF+∠ADF=90°,又DE⊥DF,可得:∠EDA+∠ADF=90°,故∠EDA=∠CDF,从而可证:△AED≌△CFD,所以可得:AE=CF,AF=BC,即可得出答案;
(2)延长ED到P,使DP=DE,连接FP,CP,利用SAS得到三角形BED与三角形CPD全等,利用全等三角形对应边相等得到BE=CP,再利用SAS得到撒尿性EDF和三角形PDF全等,利用全等三角形对应边相等得到EF=FP,利用等角的余角相等得到∠FCP为直角,在直角三角形FCP中,利用勾股定理列出关系式,等量代换即可得证.
(1)如图1,连接AD,
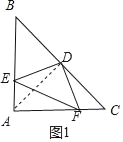
∵在Rt△ABC中,AB=AC,AD为BC边的中线,
∴∠DAC=∠BAD=∠C=45°,AD⊥BC,AD=DC,
又∵DE⊥DF,AD⊥DC,
∴∠EDA+∠ADF=∠CDF+∠FDA=90°,
∴∠EDA=∠CDF
在△AED与△CFD中,
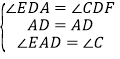 ,
,
∴△AED≌△CFD(ASA).
∴AE=CF,
同理AF=BE.
∵∠EAF=90°,
∴EF2=DE2+DF2,
∴BE2+CF2=EF2,
∴EF=![]() =13;
=13;
(2)EF2=BE2+CF2;
如图2,延长ED到P,使DP=DE,连接FP,CP,
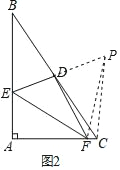
在△BED和△CPD中, 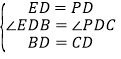 ,
,
∴△BED≌△CPD(SAS),
∴BE=CP,∠B=∠CPD,
在△EDF和△PDF中,
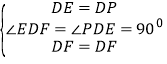 ,
,
∴△EDF≌△PDF(SAS),
∴EF=FP,
∵∠B=∠DCP,∠A=90°,
∴∠B+∠ACB=90°,
∴∠ACB+∠DCP=90°,即∠FCP=90°,
在Rt△FCP中,根据勾股定理得:CF2+CP2=PF2,
∵BE=CP,PF=EF,
∴EF2=BE2+CF2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在Rt△ABC中,∠C=90°,BC=6cm,AC=8 cm,AB=10 cm. 现有一动点P,从A点出发,沿着三角形的边AC-CB-BA运动,回到A点停止,速度为1 cm/s,设运动时间为t s.
(1)当t=_______时,△ABC的周长被线段AP平分为相等的两部分.
(2)当t=_______时,△APC的面积等于△ABC面积的一半.
(3)还有一个△DEF,∠E=90°,如图②所示,DE=4cm,DF=5cm,∠D=∠A. 在△ABC的边上,若另外有一个动点Q,与P 同时从A点出发,沿着边AB-BC-CA运动,回到点A停止. 在两点运动过程中某一时刻,恰好△APQ与△DEF全等,则点Q的运动速度 cm/s.


-
科目: 来源: 题型:
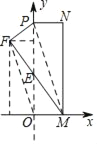
查看答案和解析>>【题目】如图,在平面直角坐标系中,长方形MNPO的边OM在x轴上,边OP在y轴上,点N的坐标为(3,9),将矩形沿对角线PM翻折,N点落在F点的位置,且FM交y轴于点E,那么点F的坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】西安市在创建文明城区的活动中,有两个长度相等的彩色砖道铺设任务,分别交给甲、乙两个施工队同时进行施工,如图是反映所铺设的彩色砖道的长度y(米)与施工时间x(小时)之间关系的部分图象,请解答下列问题:
(1)求乙队在0≤x≤6的时段内y与x的函数关系式.
(2)如果甲队施工速度不变,乙队在施工6小时后,施工速度增加到12米/小时,结果两队同时完成了任务,求甲队从开始施工到完成所铺设的彩色砖道的长度为多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售? -
科目: 来源: 题型:
查看答案和解析>>【题目】一位同学拿了两块45°的三角尺△MNK,△ACB做了一个探究活动:将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=a.
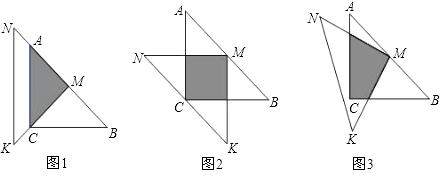
(1)如图1,两个三角尺的重叠部分为△ACM,则重叠部分的面积为 , 周长为;
(2)将图1中的△MNK绕顶点M逆时针旋转45°,得到图2,此时重叠部分的面积为 , 周长为;
(3)如果将△MNK绕M旋转到不同于图1,图2的位置,如图3所示,猜想此时重叠部分的面积为多少?并试着加以验证. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数
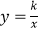 的图象经过第二象限内的点A(﹣1,m),AB⊥x轴于点B,△AOB的面积为2.若直线y=ax+b经过点A,并且经过反比例函数
的图象经过第二象限内的点A(﹣1,m),AB⊥x轴于点B,△AOB的面积为2.若直线y=ax+b经过点A,并且经过反比例函数 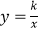 的图象上另一点C(n,一2).
的图象上另一点C(n,一2).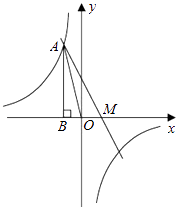
(1)求直线y=ax+b的解析式;
(2)设直线y=ax+b与x轴交于点M,求AM的长.
相关试题

