搜索
【题目】如图，直线
与x轴相交于点A，与y轴相交于点B．
（1）求A、B两点的坐标；
（2）过B点作直线BP与x轴相交于P，且使AP=2OA， 求ΔBOP的周长．
参考答案：
【答案】（1）
；（2）
或
．
【解析】
（1）把x=0，y=0代入
，即可求出A、B两点的坐标；
（2）先求出AP=3，得到点P坐标为（
,0）或（
，0），分类讨论，根据勾股定理求出BP，问题得解．
解：（1）把x=0代入得y=3，
把y=0代入得
，解得
，
∴A(
,0)，B(0,3)；
(2)∵AP=2OA，
∴AP=3，
∴点P坐标为（,0）或（，0）
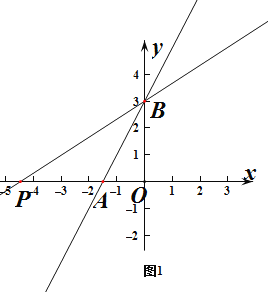
如图1，当点P坐标为（,0）时，
在
，
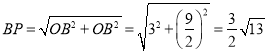
∴ ΔBOP的周长为3+
+
=；
如图2，当点P坐标为（,0）时，
在，
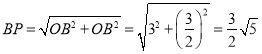
∴ ΔBOP的周长为3++=；
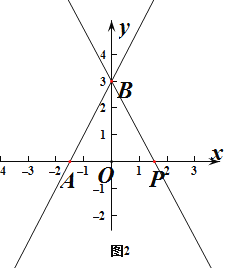
综上所述，ΔBOP的周长为或．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，某沿海城市A接到台风警报，在该市正南方向
千米有一台风中心正在B处形成，并沿着北偏东45°的BC方向以15千米/小时的速度向C移动，AD⊥BC于D，如果在距台风中心150千米的区域内都将受到台风的影响，请问：
（1）通过计算说明，台风会否影响到A市？
（2）画图计算说明，台风中心从B处出发后，经过几小时会影响到A市，对A市持续影响的时间有多少小时？在第几小时时对A市的影响最大？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在平面直角坐标系中，点A坐标为(4，4)，点B的坐标为(2，0)．
(1)求线段AB的长；
(2)点M是坐标轴上的一个点，若以AB为直角边构造直角三角形△ABM，请求出满足条件的所有点M的坐标；
(3)如图2，以点A为直角顶点作∠CAD=90°，射线AC交x轴的负半轴与点C，射线AD交y轴的负半轴与点D，当∠CAD绕点A旋转时，OCOD的值是否发生变化?若不变，直接写出它的值；若变化，直接写出它的变化范围(不要求写解题过程)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（10分）九（1）班数学兴趣小组经过市场调查，整理出某种商品在第x（1≤x≤90）天的售价与销量的相关信息如下表：
已知该商品的进价为每件30元，设销售该商品的每天利润为y元．
（1）求出y与x的函数关系式；
（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少？
（3）该商品在销售过程中，共有多少天每天销售利润不低于4800元？请直接写出结果．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知关于x的一元二次方程ax2－3x－1＝0有两个不相等的实数根，且两个实数根都在－1和0之间(不包含－1和0)，求a的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，把长方形纸片OABC放入直角坐标系中，使OA， OC分别落在x轴、y轴的正半轴上，连接AC，将
翻折，点B落在该坐标平面内，设这个落点为D，CD交x轴于点E，已知CB=8，AB=4.
(1)求AC所在直线的函数关系式;
(2)求点E的坐标和
的面积:(3)求点D的坐标，并判断点(8， -4)是否在直线OD上，说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某汽车在相距70千米的甲、乙两地往返行驶，由于行程中有一坡度均匀的小山，该汽车由甲地到乙地需用2小时30分，而从乙地到甲地需用2小时18分．若汽车在平地上的速度为30千米／时，上坡的速度为20千米／时，下坡的速度为40千米／时，求从甲地到乙地的行程中，平路、上坡路、下坡路各多少千米?
相关试题
