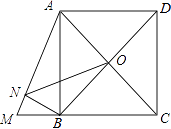
【题目】如图,正方形ABCD的边长为4,延长CB至M,使BM=2,连接AM,BN⊥AM于N,O是AC、BD的交点,连接ON,则ON的长为 
参考答案:
【答案】![]()
【解析】解:∵AB=4,BM=2,
∴AM= ![]() =2
=2 ![]() ,
,
∵∠ABM=90°,BN⊥AM,
∴△ABN∽△BNM∽△AMB,
∴AB2=AN×AM,BM2=MN×AM,
∴AN= ![]() ,MN=
,MN= ![]() ,
,
∵AB=4,CD=4,
∴AC=4 ![]() ,
,
∴AO=2 ![]() ,
,
∵ ![]() =
= ![]() =
= ![]() ,且∠CAM=∠NAO
,且∠CAM=∠NAO
∴△AON∽△AMC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴ON= ![]() .
.
所以答案是: ![]() .
.
【考点精析】掌握勾股定理的概念和正方形的性质是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】张老师驾车从家出发到植物园赏花,匀速行驶一段时间后,途中遇到堵车原地等待一会儿,然后加速行驶,到达植物园,参观结束后,张老师驾车一路匀速返回,其中x表示汽车从家出发后所用时间,y表示车离家的距离,下面能反映y与x的函数关系式的大致图象是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从﹣2,﹣
 ,
,  ,1,3五个数中任选1个数,记为a,它的倒数记为b,将a,b代入不等式组
,1,3五个数中任选1个数,记为a,它的倒数记为b,将a,b代入不等式组 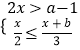 中,能使不等式组至少有两个整数解的概率是 .
中,能使不等式组至少有两个整数解的概率是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,BD平分∠ABC,延长BC到E,使得CE=CD.
求证:BD=DE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣
 )﹣2+
)﹣2+  ﹣|﹣
﹣|﹣  |+(﹣π)0﹣(﹣1)2015 .
|+(﹣π)0﹣(﹣1)2015 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,这是一个供滑板爱好者使用的U型池,该U型池可以看成是一个长方体去掉一个“半圆柱”,中间可供滑行部分的截面是半径为4 m的半圆,其边缘AB=CD=20 m,点E在CD上,CE=2 m.一滑板爱好者从A点滑到E点,则他滑行的最短路程约为____________(边缘部分的厚度忽略不计,结果保留整数.提示:482≈222).

-
科目: 来源: 题型:
查看答案和解析>>【题目】当三角形中一个内角是另一个内角的3倍时,我们称此三角形为“梦想三角形”.如果一个“梦想三角形”有一个角为108°,那么这个“梦想三角形”的最小内角的度数为_____.
相关试题

