【题目】如图,等边△ABC的边长为3,F为BC边上的动点,FD⊥AB于D,FE⊥AC于E,则DE的长为( )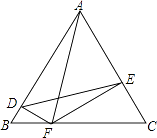
A.随F点运动,其值不变
B.随F点运动而变化,最大值为 ![]()
C.随F点运动而变化,最小值为 ![]()
D.随F点运动而变化,最小值为 ![]()
参考答案:
【答案】D
【解析】解:作AG⊥BC于G,
∵△ABC是等边三角形,
∴∠B=60°,
∴AG= ![]() AB=
AB= ![]() ,
,
∵S△ABF+S△ACF=S△ABC ,
∴ ![]() ABDF+
ABDF+ ![]() ACEF=
ACEF= ![]() BCAG,
BCAG,
∵AB=AC=BC=2,
∴DF+EF=AG= ![]() ,
,
∵△DEF中,DE<DF+EF,
∴DE的长随F点运动而变化,最小值为 ![]() .
.
故选:D.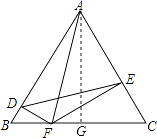
【考点精析】掌握等边三角形的性质和等边三角形的判定是解答本题的根本,需要知道等边三角形的三个角都相等并且每个角都是60°;三个角都相等的三角形是等边三角形;有一个角等于60°的等腰三角形是等边三角形.
-
科目: 来源: 题型:
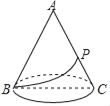
查看答案和解析>>【题目】如图,圆锥的轴截面是边长为6cm的正三角形ABC,P是母线AC的中点,则在圆锥的侧面上从B点到P点的最短路线的长为( )
A.
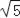 B. 2
B. 2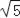 C. 3
C. 3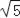 D. 4
D. 4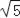
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于抛物线y=ax2﹣4ax+3a下列说法:①对称轴为x=2;②抛物线与x轴两交点的坐标分别为(1,0),(3,0);③顶点坐标为(2,﹣a);④若a<0,当x>2时,函数y随x的增大而增大,其中正确的结论有( )个.
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a,
∵S四边形ADCB=S△ACD+S△ABC= 12 b2+ 12 ab.
又∵S四边形ADCB=S△ADB+S△DCB= 12 c2+ 12 a(b﹣a)
∴ 12 b2+ 12 ab= 12 c2+ 12 a(b﹣a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a2+b2=c2 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),该抛物线的对称轴为直线x=﹣1,若点C(﹣
 ,y1),D(﹣
,y1),D(﹣  ,y2),E(
,y2),E(  ,y3)均为函数图象上的点,则y1 , y2 , y3的大小关系为 .
,y3)均为函数图象上的点,则y1 , y2 , y3的大小关系为 . 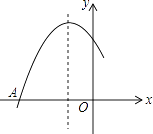
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AC=BC,∠ACB=90°,将△ABC绕点A旋转60°到△ADE的位置,点C的对应点为E,连接CD,若AC=BC=1,则CD的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣4x+1﹣p2=0.
(1)若p=2,求原方程的根;
(2)求证:无论p为何值,方程总有两个不相等的实数根.
相关试题

