【题目】在△ABC中,AC=BC,∠ACB=90°,将△ABC绕点A旋转60°到△ADE的位置,点C的对应点为E,连接CD,若AC=BC=1,则CD的长为 .
参考答案:
【答案】![]() 或=
或= ![]()
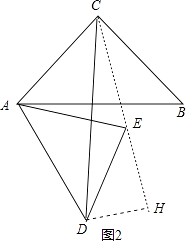
【解析】解:当△ABC绕点A逆时针旋转60°得到△ADE的位置,如图1,作CH⊥ED于H,连结CE,
则∠EAC=60°,∠AED=∠ACB=90°,AE=ED=AC=1,
∴△AEC为等边三角形,
∴∠AEC=60°,EC=CA=1,
∴∠DEC=30°,
在Rt△CEH中,CH= ![]() CE=
CE= ![]() ,EH=
,EH= ![]() CH=
CH= ![]() ,
,
∴DH=ED﹣EH=1﹣ ![]() ,
,
在Rt△CHD中,CD= ![]() =
= ![]() =
= ![]() ;
;
当△ABC绕点A顺时针旋转60°得到△ADE的位置,如图2,连结CE,作DH⊥CE于H,
则∠EAC=60°,∠AED=∠ACB=90°,AE=ED=AC=1,
∴△AEC为等边三角形,
∴∠AEC=60°,EC=CA=1,
∴∠DEC=150°,
∴∠DEH=30°,
在Rt△DEH中,DH= ![]() DE=
DE= ![]() ,EH=
,EH= ![]() DH=
DH= ![]() ,
,
∴CH=CE+EH=1+ ![]() ,
,
在Rt△CHD中,CD= ![]() =
= ![]() =
= ![]() ,
,
纵上所述,CD的长为 ![]() 或=
或= ![]() .
.
所以答案是 ![]() 或=
或= ![]() .
.
【考点精析】关于本题考查的图形的旋转,需要了解每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.旋转的方向、角度、旋转中心是它的三要素才能得出正确答案.
-
科目: 来源: 题型:
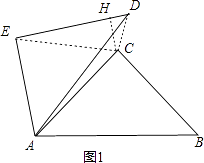
查看答案和解析>>【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a,
∵S四边形ADCB=S△ACD+S△ABC= 12 b2+ 12 ab.
又∵S四边形ADCB=S△ADB+S△DCB= 12 c2+ 12 a(b﹣a)
∴ 12 b2+ 12 ab= 12 c2+ 12 a(b﹣a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a2+b2=c2 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC的边长为3,F为BC边上的动点,FD⊥AB于D,FE⊥AC于E,则DE的长为( )
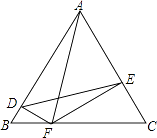
A.随F点运动,其值不变
B.随F点运动而变化,最大值为
C.随F点运动而变化,最小值为
D.随F点运动而变化,最小值为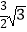
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),该抛物线的对称轴为直线x=﹣1,若点C(﹣
 ,y1),D(﹣
,y1),D(﹣  ,y2),E(
,y2),E(  ,y3)均为函数图象上的点,则y1 , y2 , y3的大小关系为 .
,y3)均为函数图象上的点,则y1 , y2 , y3的大小关系为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣4x+1﹣p2=0.
(1)若p=2,求原方程的根;
(2)求证:无论p为何值,方程总有两个不相等的实数根. -
科目: 来源: 题型:
查看答案和解析>>【题目】⑴ 阅读理解:我们知道在直角三角形中,有无数组勾股数,例如:5、12、13;9、40、41;……但其中也有一些特殊的勾股数,例如:3、4、5;是三个连续正整数组成的勾股数.
解决问题:① 在无数组勾股数中,是否存在三个连续偶数能组成勾股数?
答: ,若存在,试写出一组勾股数: .
② 在无数组勾股数中,是否还存在其它的三个连续正整数能组成勾股数?若存在,求出勾股数,若不存在,说明理由.
③ 在无数组勾股数中,是否存在三个连续奇数能组成勾股数?若存在,求出勾股数,若不存在,说明理由.
⑵ 探索升华:是否存在锐角△ABC三边也为连续正整数;且同时还满足:∠B>∠C>∠A;∠ABC=2∠BAC?若存在,求出△ABC三边的长;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学有一块四边形的空地ABCD,如图所示,为了绿化环境,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m.
(1)求出空地ABCD的面积.
(2)若每种植1平方米草皮需要200元,问总共需投入多少元?

相关试题

