【题目】关于x、y的单项式2axcy与单项式3bx3y是同类项,并且2axcy+3bx3y=0 ,当m 的倒数是-1,n的相反数是 ![]() 时,求
时,求 ![]() 的值。
的值。
参考答案:
【答案】解:∵m的倒数是-1,n的相反数是 ![]() ,
,
∴m=-1,n= ![]() ,
,
∵关于x、y的单项式2axcy与单项式3bx3y是同类项,
∴c=3,
∵2axcy+3bx3y=0,
∴2a+3b=0,
∴(2a+3b)99+mc-nc
=099+(-1)3- ![]()
= ![]()
【解析】根据倒数,相反数的定义得出m=-1,n= ![]() ,根据同类项的定义相同字母的指数相同得出c=3,根据合并同类项的法则,只把系数相加减及2axcy+3bx3y=0 ,从而得出2a+3b=0,然后把m,n及2a+3b的值代入代数式,根据乘方的意义及有理数的加减法法则即可算出结果。
,根据同类项的定义相同字母的指数相同得出c=3,根据合并同类项的法则,只把系数相加减及2axcy+3bx3y=0 ,从而得出2a+3b=0,然后把m,n及2a+3b的值代入代数式,根据乘方的意义及有理数的加减法法则即可算出结果。
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解南山荔枝的销售情况,某部门对该市场的三种荔枝品种A、B、C在6月上半月的销售进行调查统计,绘制成如下两个统计图(均不完整).请你结合图中的信息,解答下列问题:
(1)该市场6月上半月共销售这三种荔枝多少吨?
(2)补全图1的统计图并计算图2中A所在扇形的圆心角的度数.
(3)某商场计划六月下半月进货A、B、C三种荔枝共300千克,根据该市场6月上半月的销售情况,求该商场应购进C品种荔枝多少千克比较合理?
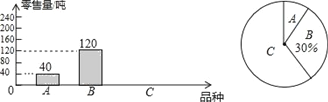
(图1) (图2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】将若干张长为20里面、宽为10里面的长方形白纸,按图所示的方法粘合起来,粘合部分的宽为2厘米.
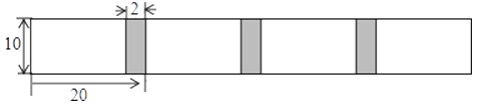
(1)求2张白纸贴合后的总长度;那么3张白纸粘合后的总长度呢?4张呢?
(2)设a张白纸粘合后的总长度为b里面,写出b与a之间的关系式,并求当a=100时,b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线与x轴交于A(1,0),B(﹣3,0)两点,与y轴交于点C(0,3),抛物线的顶点为P,连接AC.
(1)求此抛物线的解析式;
(2)在抛物线上找一点D,使得DC与AC垂直,且直线DC与x轴交于点Q,求点D的坐标;
(3)抛物线对称轴上是否存在一点M,使得
 ,若存在,求出M点坐标;若不存在,请说明理由.
,若存在,求出M点坐标;若不存在,请说明理由.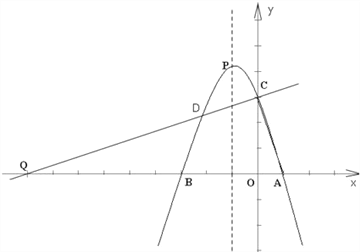
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面内,下列说法正确的是( )
A. 没有公共点的两条线段平行
B. 没有公共点的两条射线平行
C. 不垂直的两条直线一定互相平行
D. 不相交的两条直线一定互相平行
-
科目: 来源: 题型:
查看答案和解析>>【题目】操作:某数学兴趣小组在研究用一副三角板拼角时,小明、小亮分别拼出图1、图2所示的两种图形,如图1,小明把30°和90°的角按如图1方式拼在一起;小亮把30°和90°的角按如图2方式拼在一起,并在各自所拼的图形中分别作出∠AOB、∠COD的平分线OE、OF.小明很容易地计算出图1中∠EOF=60°.

计算:请你计算出图2中∠EOF=度.
归纳:通过上面的计算猜一猜,当有公共顶点的两个角∠α、∠β有一条边重合,且这两个角在公共边的异侧时,则这两个角的平分线所夹的角= . (用含α、β的代数式表示)
拓展:小明把图1中的三角板AOB绕点O顺时针旋转90°后得到图3,小亮把图2中的三角板AOB绕点O顺时针旋转90°后得到图4(两图中的点O、B、D在同一条直线上).在图3中,易得到∠EOF=∠DOF﹣∠BOE= ∠COD﹣
∠COD﹣  ∠AOB=45°﹣15°=30°;仿照图3的作法,请你通过计算,求出图4中∠EOF的度数(写出解答过程).
∠AOB=45°﹣15°=30°;仿照图3的作法,请你通过计算,求出图4中∠EOF的度数(写出解答过程).
反思:通过上面的拓展猜一猜,当有公共顶点的两个角∠α、∠β(∠α>∠β)有一条边重合,且这两个角在公共边的同侧时,则这两个角的平分线所夹的角= . -
科目: 来源: 题型:
查看答案和解析>>【题目】下列表示平行线的方法正确的是( )
A. ab∥cd B. A∥B C. a∥B D. a∥b
相关试题

