【题目】在平面直角坐标系中,抛物线![]() 与x轴交于点A(-4,0)、B(6,0)两点,与y轴交于点C.
与x轴交于点A(-4,0)、B(6,0)两点,与y轴交于点C.
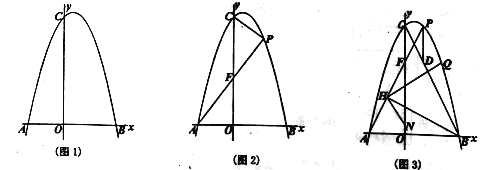
(1)如图l,求抛物线的解析式;
(2)如图2,点P为第一象限抛物线上一点,连接PC、PA,PA交y轴于点F,设点P的横坐标为t,△CPF的面积为S.求S与t的函数关系式(不要求写出自变量t的取值范围);
(3)如图3,在(2)的条件下,连接BC,过点P作PD//y轴变BC于点D,点H为AF中点,且点N(0,1),连接NH、BH,将∠NHB绕点H逆时针旋转,使角的一条边H落在射线HF上,另一条边HN变抛物线于点Q,当BH=BD时,求点Q坐标.
参考答案:
【答案】(1)抛物线的解析式为![]() ;
;
(2)S与t的函数关系式为![]() ;
;
(3)点Q坐标为(4,8).
【解析】试题分析:(1)直接用代入法求函数的解析式;(2)过点P作PR⊥y轴,交y轴于点R,过点P作PL⊥AB于点L,则点P(t, ![]() ),在Rt△PAL中,因为PL=
),在Rt△PAL中,因为PL=![]() AL=
AL= ![]() ,所以tan∠PAL=
,所以tan∠PAL=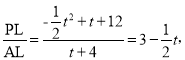 在Rt△FAO中,所以tan∠FAO=
在Rt△FAO中,所以tan∠FAO= ![]() , 所以OF=12-2t,所以CF=CO- OF=12-(12-2t)=2t,所以
, 所以OF=12-2t,所以CF=CO- OF=12-(12-2t)=2t,所以![]() ;(3)延长PD交x轴于点L,取OA的中点K,连接HK,过点H作HG⊥y轴于点G,OF=12-2t点H为AF的中点 HK ⊥OA ,所以HK=
;(3)延长PD交x轴于点L,取OA的中点K,连接HK,过点H作HG⊥y轴于点G,OF=12-2t点H为AF的中点 HK ⊥OA ,所以HK=![]() 6-t=BL,因为HK=BL BH=BD ,所以△BHK≌△DBL ,所以BK=DL=8,直线BC的解析式为
6-t=BL,因为HK=BL BH=BD ,所以△BHK≌△DBL ,所以BK=DL=8,直线BC的解析式为![]() ∴点D
∴点D![]() ,DL=12-2t =8 t=2 ,所以点P(2,12),则点H(-2,4),tan∠AHK=tan∠HBK=
,DL=12-2t =8 t=2 ,所以点P(2,12),则点H(-2,4),tan∠AHK=tan∠HBK=![]() ,所以∠AHK=∠HBK ,∴∠AHB=90°,又因为∠NHB=∠PHQ ,所以∠NHQ=90°,过点Q作QM⊥HG于点M,所以∠HNG=∠QHM ,又因为点N(0,1),HG=2,所以GN=3,tan∠HNG=tan∠QHM =
,所以∠AHK=∠HBK ,∴∠AHB=90°,又因为∠NHB=∠PHQ ,所以∠NHQ=90°,过点Q作QM⊥HG于点M,所以∠HNG=∠QHM ,又因为点N(0,1),HG=2,所以GN=3,tan∠HNG=tan∠QHM =![]() ,
, ![]() ,设点Q(
,设点Q(![]() ,
,![]() ) ,则QM=
) ,则QM=![]() -4=
-4=![]() ,所以HM=
,所以HM= ![]() +2 ,所以
+2 ,所以  ,解得:
,解得: ![]() ,所以 ∴点Q(4,8);
,所以 ∴点Q(4,8);
试题解析:
(1)解∵抛物线![]() 过点A(-4,0),B(6,0)
过点A(-4,0),B(6,0)
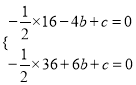 解得
解得![]()
∴抛物线解析式为![]()
(2)过点P作PR⊥y轴,交y轴于点R,过点P作PL⊥AB于点L,如图所示:
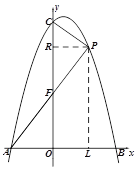
则点P(t, ![]() ),在Rt△PAL中
),在Rt△PAL中
∵PL=![]() AL=
AL= ![]()
∴tan∠PAL= 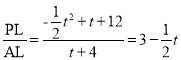
在Rt△FAO中,
∴tan∠FAO= ![]() ,
,
∴OF=12-2t
∴CF=CO- OF=12-(12-2t)=2t
∴![]()
(3)延长PD交x轴于点L,取OA的中点K,连接HK,过点H作HG⊥y轴于点G,如图所示:
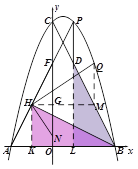
OF=12-2t点H为AF的中点 HK ⊥OA
∴HK=![]() 6-t=BL
6-t=BL
∵HK=BL BH=BD
∴△BHK≌△DBL
∴BK=DL=8
直线BC的解析式为![]()
∴点D![]()
DL=12-2t =8 t=2
∴点P(2,12)
∴点H(-2,4)
tan∠AHK=tan∠HBK=
∴∠AHK=∠HBK
∴∠AHB=90°
∵∠NHB=∠PHQ
∴∠NHQ=90°,
过点Q作QM⊥HG于点M,
∴∠HNG=∠QHM
∵点N(0,1),HG=2,
∴GN=3,tan∠HNG=tan∠QHM =![]() ,
, ![]()
设点Q(![]() ,
,![]() )
)
QM=![]() -4=
-4=![]()
HM= ![]() +2
+2
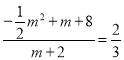 ,
,
![]()
∴点Q(4,8)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列图案均是长度相同的火柴按一定的规律拼搭而成:第1个图案需7根火柴,第2个图案需13根火柴,…,依此规律,第11个图案需( )根火柴.

A.156
B.157
C.158
D.159 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)如图①,BF垂直CE于点F,交CD于点G,试说明AE=CG;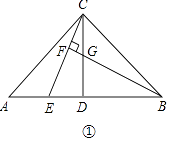
(2)如图②,作AH垂直于CE的延长线,垂足为H,交CD的延长线于点M,则图中与BE相等的线段是 , 并说明理由.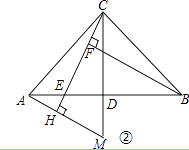
-
科目: 来源: 题型:
查看答案和解析>>【题目】把抛物线y=﹣2x2向左平移3个单位,再向上平移2个单位后的抛物线的解析式为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)化简:2x2﹣[ (xy﹣x2)+8xy]﹣
(xy﹣x2)+8xy]﹣  xy
xy
(2)化简并求值: x﹣2(x﹣
x﹣2(x﹣  y2)+(﹣
y2)+(﹣  x+
x+  y2),其中:x=﹣1,y=
y2),其中:x=﹣1,y=  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果m、n是方程x2+2x﹣5=0的两个实数根,则m2+3m+n=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各近似数中,精确度一样的是( )
A.0.28与0.280
B.0.70与0.07
C.5百万与500万
D.1.1×103与1100
相关试题

