【题目】如图,在△ABC中,以BC为直径的圆交AC于点D,∠ABD=∠ACB. 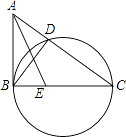
(1)求证:AB是圆的切线;
(2)若点E是BC上一点,已知BE=4,tan∠AEB= ![]() ,AB:BC=2:3,求圆的直径.
,AB:BC=2:3,求圆的直径.
参考答案:
【答案】
(1)证明:∵BC是直径,
∴∠BDC=90°,
∴∠ACB+∠DBC=90°,
∵∠ABD=∠ACB,
∴∠ABD+∠DBC=90°
∴∠ABC=90°
∴AB⊥BC,
∴AB是圆的切线
(2)解:在RT△AEB中,tan∠AEB= ![]() ,
,
∴ ![]() =
= ![]() ,即AB=
,即AB= ![]() BE=
BE= ![]() ,
,
在RT△ABC中, ![]() =
= ![]() ,
,
∴BC= ![]() AB=10,
AB=10,
∴圆的直径为10
【解析】(1)欲证明AB是圆的切线,只要证明∠ABC=90°即可.(2)在RT△AEB中,根据tan∠AEB= ![]() ,求出BC,在RT△ABC中,根据
,求出BC,在RT△ABC中,根据 ![]() =
= ![]() 求出AB即可.
求出AB即可.
【考点精析】关于本题考查的切线的判定定理,需要了解切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛.赛后组委会整理参赛同学的成绩,并制作了如下不完整的频数分布表和频数分布直方图.
分数段(分数为x分)
频数
百分比
60≤x<70
8
20%
70≤x<80
a
30%
80≤x≤90
16
b%
90≤x<100
4
10%
请根据图表提供的信息,解答下列问题:
(1)表中的a= , b=;请补全频数分布直方图;
(2)若用扇形统计图来描述成绩分布情况,则分数段70≤x<80对应扇形的圆心角的度数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一辆汽车从P处出发,先沿北偏东60°的方向行驶到达A处后,接着向正南方向行驶100(
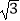 +1)千米到达B处.在B处观测到出发时所在的P处在北偏西45°方向上,P,A两处相距多少千米?
+1)千米到达B处.在B处观测到出发时所在的P处在北偏西45°方向上,P,A两处相距多少千米?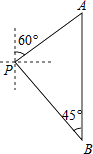
-
科目: 来源: 题型:
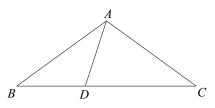
查看答案和解析>>【题目】如图,一长方形花园用来种植菊花和郁金香,其余作为休息区;
(1)求种植菊花和郁金香的面积;
(2)当
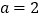 m,
m,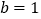 m时,种植菊花和郁金香的面积是多少m2?
m时,种植菊花和郁金香的面积是多少m2?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是BC边上一点,AD=BD,AB=AC=CD,求∠BAC的度数.
-
科目: 来源: 题型:
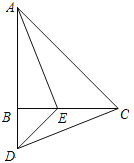
查看答案和解析>>【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.
① 求证:△ABE≌△CBD;
② 若∠CAE=30°,求∠BDC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场.某车行经营的A型车2016年4月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年4月份与去年4月份卖出的A型车数量相同,则今年4月份A型车销售总额将比去年4月份销售总额增加25%.(A、B两种型号车今年的进货和销售价格如下表所示)
A型车
B型车
进货价格(元/辆)
1100
1400
销售价格(元/辆)
今年的销售价格
2400
(1)求今年4月份A型车每辆销售价多少元(用列方程进行解答);
(2)该车行计划5月份新进一批A型车和B型车共50辆,设购进的A型车为x辆,获得的总利润为y元,请写出y与x之间的函数关系式;
(3)在(2)的条件下,若B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最大?最大利润是多少?
相关试题

