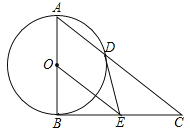
【题目】如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)求证:BC2=2CDOE;
(3)若![]() ,求OE的长.
,求OE的长.
参考答案:
【答案】(1)DE为⊙O的切线,理由见解析
(2)证明见解析
(3)OE=![]()
【解析】试题分析:(1)连接OD,BD,由直径所对的圆周角是直角得到∠ADB为直角,可得出△BCD为直角三角形,E为斜边BC的中点,由直角三角形斜边上的中线等于斜边的一半,得到CE=DE,从而得∠C=∠CDE,再由OA=OD,得∠A=∠ADO,由Rt△ABC中两锐角互余,从而可得∠ADO与∠CDE互余,可得出∠ODE为直角,即DE垂直于半径OD,可得出DE为⊙O的切线;
(2)由已知可得OE是△ABC的中位线,从而有AC=2OE,再由∠C=∠C,∠ABC=∠BDC,可得△ABC∽△BDC,根据相似三角形的对应边的比相等,即可证得;
(3)在直角△ABC中,利用勾股定理求得AC的长,根据三角形中位线定理OE的长即可求得.
试题解析:(1)DE为⊙O的切线,理由如下:
连接OD,BD,
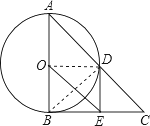
∵AB为⊙O的直径,
∴∠ADB=90°,
在Rt△BDC中,E为斜边BC的中点,
∴CE=DE=BE=![]() BC,
BC,
∴∠C=∠CDE,
∵OA=OD,
∴∠A=∠ADO,
∵∠ABC=90°,
∴∠C+∠A=90°,
∴∠ADO+∠CDE=90°,
∴∠ODE=90°,
∴DE⊥OD,又OD为圆的半径,
∴DE为⊙O的切线;
(2)∵E是BC的中点,O点是AB的中点,
∴OE是△ABC的中位线,
∴AC=2OE,
∵∠C=∠C,∠ABC=∠BDC,
∴△ABC∽△BDC,
∴![]() ,即BC2=ACCD.
,即BC2=ACCD.
∴BC2=2CDOE;
(3)解:∵cos∠BAD=![]() ,
,
∴sin∠BAC=![]() ,
,
又∵BE=![]() ,E是BC的中点,即BC=
,E是BC的中点,即BC=![]() ,
,
∴AC=![]() .
.
又∵AC=2OE,
∴OE=![]() AC=
AC=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题:
(1)﹣11﹣(﹣3)×6
(2)﹣3.5÷ ×(﹣0.75)
×(﹣0.75)
(3)﹣32+1+4× ﹣|﹣1
﹣|﹣1  |×(﹣0.5)2 .
|×(﹣0.5)2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】将方程3x2﹣x=﹣2(x+1)2化成一般形式后,一次项系数为( )
A.﹣5
B.5
C.﹣3
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】近几年兴义市加大中职教育投入力度,取得了良好的社会效果。某校随机调查了九年级a名学生升学意向,并根据调查结果绘制如图的两幅不完整的统计图。
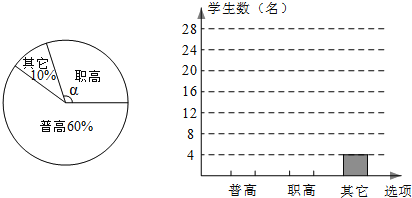
请你根据图中信息解答下列问题:
(1)a= ;
(2)扇形统计图中,“职高”对应的扇形的圆心角α= ;
(3)请补全条形统计图;
(4)若该校九年级有学生900名,估计该校共有多少名毕业生的升学意向是职高。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:(注:获利=售价-进价)

(1)若商店计划销售完这批商品后能获利1 100元,请问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4300元,且销售完这批商品后获利多于1260元,请问有哪几种购货方案?并指出获利最大的购货方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是
A. a3·a2=a6 B. (x3)3=x6
C. x5+x5=x10 D. (-ab)5÷(-ab)2=-a3b3
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题:①无理数都是无限小数;②
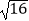 的平方根是±4;③等腰三角形的对称轴是它顶角的平分线;④三角形三边垂直平分线的交点一定在这个三角形的内部,正确的有( )
的平方根是±4;③等腰三角形的对称轴是它顶角的平分线;④三角形三边垂直平分线的交点一定在这个三角形的内部,正确的有( )
A.1个
B.2个
C.3个
D.4个
相关试题

