【题目】如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P,Q分别是边OB,OA上的动点,记∠OPM=α,∠OQN=β,当MP+PQ+QN最小时,则关于α,β的数量关系正确的是( )

A. β﹣α=60° B. β+α=210° C. β﹣2α=30° D. β+2α=240°
参考答案:
【答案】B
【解析】
如图,作M关于OB的对称点M′,N关于OA的对称点N′,连接M′N′交OA于Q,交OB于P,则MP+PQ+QN最小易知∠OPM=∠OPM′=∠NPQ,∠OQP=∠AQN′=∠AQN,KD∠OQN=180°-30°-∠ONQ,∠OPM=∠NPQ=30°+∠OQP,∠OQP=∠AQN=30°+∠ONQ,由此即可解决问题.
如图,作M关于OB的对称点M′,N关于OA的对称点N′,连接M′N′交OA于Q,交OB于P,则MP+PQ+QN最小,
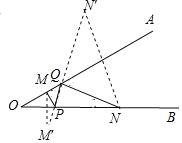
易知∠OPM=∠OPM′=∠NPQ,∠OQP=∠AQN′=∠AQN,
∵∠OQN=180°-30°-∠ONQ,∠OPM=∠NPQ=30°+∠OQP,∠OQP=∠AQN=30°+∠ONQ,
∴α+β=180°-30°-∠ONQ+30°+30°+∠ONQ=210°.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:
(1)在同一平面内,不相交的两条直线一定平行.(2)在同一平面内,不相交的两条线段一定平行.(3)相等的角是对顶角.(4)两条直线被第三条直线所截,同位角相等.(5)两条平行线被第三条直线所截,一对内错角的角平分线互相平行.其中,正确说法的个数是( )
A. 1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究同一平面直角坐标系中系数互为倒数的正、反比例函数y=
 x与y=
x与y= 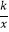 (k≠0)的图象性质.
(k≠0)的图象性质.
小明根据学习函数的经验,对函数y= x与y=
x与y= 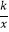 ,当k>0时的图象性质进行了探究.
,当k>0时的图象性质进行了探究.
下面是小明的探究过程: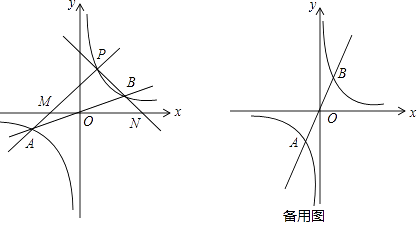
(1)如图所示,设函数y= x与y=
x与y= 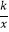 图象的交点为A,B,已知A点的坐标为(﹣k,﹣1),则B点的坐标为;
图象的交点为A,B,已知A点的坐标为(﹣k,﹣1),则B点的坐标为;
(2)若点P为第一象限内双曲线上不同于点B的任意一点.
①设直线PA交x轴于点M,直线PB交x轴于点N.求证:PM=PN.
证明过程如下,设P(m, ),直线PA的解析式为y=ax+b(a≠0).
),直线PA的解析式为y=ax+b(a≠0).
则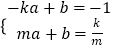 ,
,
解得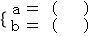
∴直线PA的解析式为
请你把上面的解答过程补充完整,并完成剩余的证明.
②当P点坐标为(1,k)(k≠1)时,判断△PAB的形状,并用k表示出△PAB的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图.从下列四个条件:①BC=B′C,②AC=A′C,③∠A′CA=∠B′CB,④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )
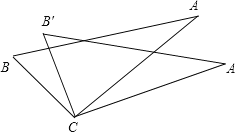
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
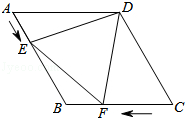
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E,F同时由A,C两点出发,分别沿AB,CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为( )
A.1
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点
 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则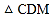 周长的最小值为
周长的最小值为


A. 6 B. 8 C. 10 D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从①∠1=∠2;②∠C=∠D;③∠A=∠F三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )

A. 0 B. 1 C. 2 D. 3
相关试题

