【题目】有这样一个问题:探究同一平面直角坐标系中系数互为倒数的正、反比例函数y= ![]() x与y=
x与y= ![]() (k≠0)的图象性质.
(k≠0)的图象性质.
小明根据学习函数的经验,对函数y= ![]() x与y=
x与y= ![]() ,当k>0时的图象性质进行了探究.
,当k>0时的图象性质进行了探究.
下面是小明的探究过程: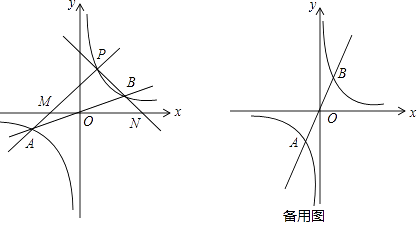
(1)如图所示,设函数y= ![]() x与y=
x与y= ![]() 图象的交点为A,B,已知A点的坐标为(﹣k,﹣1),则B点的坐标为;
图象的交点为A,B,已知A点的坐标为(﹣k,﹣1),则B点的坐标为;
(2)若点P为第一象限内双曲线上不同于点B的任意一点.
①设直线PA交x轴于点M,直线PB交x轴于点N.求证:PM=PN.
证明过程如下,设P(m, ![]() ),直线PA的解析式为y=ax+b(a≠0).
),直线PA的解析式为y=ax+b(a≠0).
则 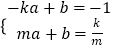 ,
,
解得 ![]()
∴直线PA的解析式为 ![]()
请你把上面的解答过程补充完整,并完成剩余的证明.
②当P点坐标为(1,k)(k≠1)时,判断△PAB的形状,并用k表示出△PAB的面积.
参考答案:
【答案】
(1)(k,1)
(2)
②解:由①可知,在△PMN中,PM=PN,
∴△PMN为等腰三角形,且MH=HN=k.
当P点坐标为(1,k)时,PH=k,
∴MH=HN=PH,
∴∠PMH=∠MPH=45°,∠PNH=∠NPH=45°,
∴∠MPN=90°,即∠APB=90°,
∴△PAB为直角三角形.
当k>1时,如图1,
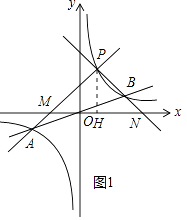
S△PAB=S△PMN﹣S△OBN+S△OAM,
= ![]() MNPH﹣
MNPH﹣ ![]() ONyB+
ONyB+ ![]() OM|yA|,
OM|yA|,
= ![]() ×2k×k﹣
×2k×k﹣ ![]() (k+1)×1+
(k+1)×1+ ![]() (k﹣1)×1,
(k﹣1)×1,
=k2﹣1;
当0<k<1时,如图2,
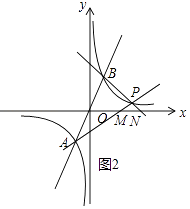
S△PAB=S△OBN﹣S△PMN+S△OAM,
= ![]() ONyB﹣k2+
ONyB﹣k2+ ![]() OM|yA|,
OM|yA|,
= ![]() (k+1)×1﹣k2+
(k+1)×1﹣k2+ ![]() (1﹣k)×1,
(1﹣k)×1,
=1﹣k2
【解析】解:(1)由正、反比例函数图象的对称性可知,点A、B关于原点O对称,
∵A点的坐标为(﹣k,﹣1),
∴B点的坐标为(k,1).
所以答案是:(k,1).
2)①证明过程如下,设P(m, ![]() ),直线PA的解析式为y=ax+b(a≠0).
),直线PA的解析式为y=ax+b(a≠0).
则 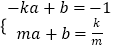 ,
,
解得: 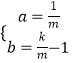 ,
,
∴直线PA的解析式为y= ![]() x+
x+ ![]() ﹣1.
﹣1.
当y=0时,x=m﹣k,
∴M点的坐标为(m﹣k,0).
过点P作PH⊥x轴于H,如图1所示,
∵P点坐标为(m, ![]() ),
),
∴H点的坐标为(m,0),
∴MH=xH﹣xM=m﹣(m﹣k)=k.
同理可得:HN=k.
∴MH=HN,
∴PM=PN.
所以答案是: 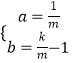 ;y=
;y= ![]() x+
x+ ![]() ﹣1.
﹣1.
【考点精析】解答此题的关键在于理解反比例函数的图的相关知识,掌握反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点,以及对反比例函数的性质的理解,了解性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
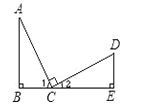
A. ∠1=∠2 B. ∠A =∠2 C. △ABC≌△CED D. ∠A与∠D互为余角
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上 A点表示的数是 a ,B 点表示的数是b ,且 ab满足|a 8|b-220.动线段 CD=4(点 D 在点 C 的右侧),从点 C与点 A重合的位置出发,以每秒 2 个单位的速度向右运动,运动时间为 t秒.
(1)求a,b的值, 运动过程中,点 D 表示的数是多少,(用含有 t 的代数式表示)
(2)在 B、C、D 三个点中,其中一个点是另外两个点为端点的线段的中点,求 t 的值;
(3)当线段 CD 在线段 AB上(不含端点重合)时,如图,图中所有线段的和记作为 S, 则 S的值是否随时间 t 的变化而变化?若变化,请说明理由;若不变,请求出 S值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:
(1)在同一平面内,不相交的两条直线一定平行.(2)在同一平面内,不相交的两条线段一定平行.(3)相等的角是对顶角.(4)两条直线被第三条直线所截,同位角相等.(5)两条平行线被第三条直线所截,一对内错角的角平分线互相平行.其中,正确说法的个数是( )
A. 1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图.从下列四个条件:①BC=B′C,②AC=A′C,③∠A′CA=∠B′CB,④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )
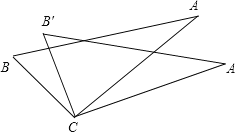
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P,Q分别是边OB,OA上的动点,记∠OPM=α,∠OQN=β,当MP+PQ+QN最小时,则关于α,β的数量关系正确的是( )

A. β﹣α=60° B. β+α=210° C. β﹣2α=30° D. β+2α=240°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E,F同时由A,C两点出发,分别沿AB,CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为( )
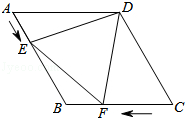
A.1
B.
C.
D.
相关试题

