【题目】如图,△ABC中,CD⊥AB于点D,⊙D经过点B,与BC交于点E,与AB交与点F.已知tanA= ![]() ,cot∠ABC=
,cot∠ABC= ![]() ,AD=8.
,AD=8.
(1)求⊙D的半径;
(2)求CE的长.
参考答案:
【答案】
(1)
【答案】解:∵CD⊥AB,AD=8,tanA= ![]() ,
,
在Rt△ACD中,tanA= ![]() =
= ![]() ,AD=8,CD=4,
,AD=8,CD=4,
在Rt△CBD,cot∠ABC= ![]() =
= ![]() ,BD=3,
,BD=3,
∴⊙D的半径为3
(2)
解:过圆心D作DH⊥BC,垂足为H,
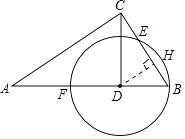
∴BH=EH,
在Rt△CBD中∠CDB=90°,BC= ![]() =5,cos∠ABC=
=5,cos∠ABC= ![]() =
= ![]() ,
,
在Rt△BDH中,∠BHD=90°,cos∠ABC= ![]() =
= ![]() ,BD=3,BH=
,BD=3,BH= ![]() ,
,
∵BH=EH,
∴BE=2BH= ![]() ,
,
∴CE=BC﹣BE=5﹣ ![]() =
= ![]() .
.
【解析】(1)根据三角函数的定义得出CD和BD,从而得出⊙D的半径;
(2)过圆心D作DH⊥BC,根据垂径定理得出BH=EH,由勾股定理得出BC,再由三角函数的定义得出BE,从而得出CE即可.
【考点精析】认真审题,首先需要了解垂径定理(垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧),还要掌握解直角三角形(解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法))的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知定点A(1,0)和B(0,1).

(1)如图1,若动点C在x轴上运动,则使△ABC为等腰三角形的点C有几个?
(2)如图2,过点A,B向过原点的直线l作垂线,垂足分别为M、N,试判断线段AM、BN、MN之间的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P为正方形ABCD的对角线BD上任一点,过点P作PE⊥BC,PF⊥CD,垂足分别为点E、F,连接EF,下列结论①△FPD是等腰直角三角形;②AP=EF;③AD=PD;④∠PFE=∠BAP,其中正确的结论是(请填序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是AB中点,联结CD.
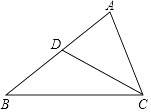
(1)若AB=10且∠ACD=∠B,求AC的长.
(2)过D点作BC的平行线交AC于点E,设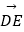 =
=  ,
, 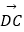 =
= 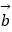 ,请用向量
,请用向量  、
、 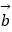 表示
表示 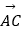 和
和 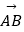 (直接写出结果)
(直接写出结果) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,拦水坝的横断面为梯形ABCD,AB∥CD,坝顶宽DC为6米,坝高DG为2米,迎水坡BC的坡角为30°,坝底宽AB为(8+2
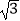 )米.
)米. 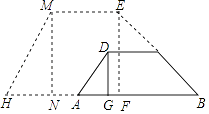
(1)求背水坡AD的坡度;
(2)为了加固拦水坝,需将水坝加高2米,并且保持坝顶宽度不变,迎水坡和背水坡的坡度也不变,求加高后坝底HB的宽度. -
科目: 来源: 题型:
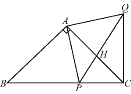
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=90°,点P是BC上的一动点,AP=AQ,∠PAQ=90°,连接CQ.
(1)求证:CQ⊥BC.
(2)△ACQ能否是直角三角形?若能,请直接写出此时点P的位置;若不能,请说明理由.
(3)当点P在BC上什么位置时,△ACQ是等腰三角形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD,点E在CB的延长线上,联结AE、DE,DE与边AB交于点F,FG∥BE且与AE交于点G.
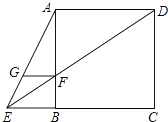
(1)求证:GF=BF.
(2)在BC边上取点M,使得BM=BE,联结AM交DE于点O.求证:FOED=ODEF.
相关试题

