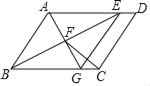
【题目】如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,过点A作BE的垂线交BE于点F,交BC于点G,连接EG,求证:四边形ABGE是菱形.
参考答案:
【答案】见解析.
【解析】
先证明AB=AE,由ASA证明△ABF≌△GBF,得出AB=GB,因此AE=GB,证出四边形ABGE是平行四边形,即可得出结论;
证明:∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵四边形ABCD是平行四边形
∴AD∥BC且AD=BC,
∴∠CBE=∠AEB,
∴∠ABE=∠AEB=∠CBE,
∴AB=AE,
∵AF⊥BE,
∴∠AFB=∠GFB=90°,
在△ABF和△GBF中,
 ,
,
∴△ABF≌△GBF(ASA),
∴AB=GB,
∴AE=GB,
又∵AD∥BC,
∴四边形ABGE是平行四边形,
又∵AB=GB,
∴四边形ABGE是菱形;
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:OA⊥OC,∠AOB:∠AOC=2:3,画出图形,并求∠BOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,点O是对角线AC的中点,点M为BC上一点,连接AM,且AB=AM,点E为BM中点,AF⊥AB,连接EF,延长FO交AB于点N.
(1)若BM=4,MC=3,AC=
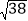 ,求AM的长度;
,求AM的长度;(2)若∠ACB=45°,求证:AN+AF=
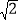 EF.
EF.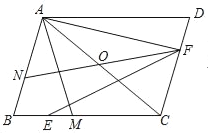
-
科目: 来源: 题型:
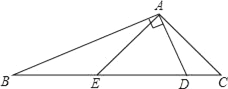
查看答案和解析>>【题目】如图.△ABC中,∠C=2∠B,D是BC上一点,且AD⊥AB,点E是BD的中点,连结AE.
(1)求证:BD=2AC;
(2)若AE=6.5,AD=5,那么△ABE的周长是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=2,AO=BO,P是直线CO上的一个动点,∠AOC=60°,当△PAB是以BP为直角边的直角三角形时,AP的长为( )
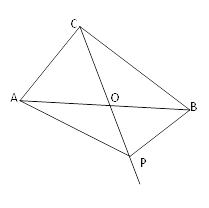
A.
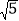 ,1,2 B.
,1,2 B. 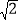 ,
,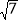 ,2 C.
,2 C.  ,
,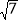 ,1 D.
,1 D. 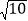 ,2
,2 -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的文字,解答问题:大家知道
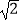 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此 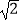 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用 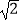 ﹣1来表示
﹣1来表示 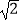 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为 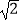 的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵22<(
的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵22<( 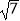 )2<32 , 即2<
)2<32 , 即2< 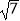 <3,∴
<3,∴ 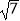 的整数部分为2,小数部分为(
的整数部分为2,小数部分为( 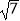 ﹣2). 请解答:
﹣2). 请解答:
(1)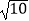 的整数部分是 , 小数部分是
的整数部分是 , 小数部分是
(2)如果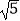 的小数部分为a,
的小数部分为a, 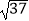 的整数部分为b,求a+b﹣
的整数部分为b,求a+b﹣ 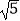 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,CD与CE分别是斜边AB上的高与中线,则下列结论:①BE=BC;②∠DCB=∠A;③∠DCB=∠ACE;④
 ,其中正确的结论是_____.
,其中正确的结论是_____.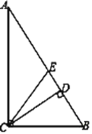
相关试题

