【题目】如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,求△DCE的面积.

参考答案:
【答案】答案见解析
【解析】由旋转的性质得出△ACE≌△ABD得出AE=AD=5.CE=BD=6.∠DAE=60°,得出△ADE是等边三角形,因此DE=AD=5.作EH⊥CD垂足为H.设DH=x,由勾股定理得出方程,解方程求出DH,由勾股定理求出EH,即可得出△DCE的面积.
作EH⊥CD垂足为H.
由旋转的性质得出△ACE≌△ABD,
所以,AE=AD=5.CE=BD=6.∠DAE=60°,
所以,△ADE是等边三角形,
所以,DE=AD=5.
设DH=x,由勾股定理得![]() ,
,
解得x=![]() ,
,
所以,S△DCE=![]() =
=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AB=2,E是AD边上一点(点E与点A,D不重合).BE的垂直平分线交AB于M,交DC于N.

(1)设AE=x,四边形ADNM的面积为S,写出S关于x的函数关系式;
(2)当AE为何值时,四边形ADNM的面积最大?最大值是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】在解方程组
 时,由于粗心,甲看错了方程组中的a,而得到方程组的解为
时,由于粗心,甲看错了方程组中的a,而得到方程组的解为 ,乙看错了方程组中的b,而得到方程组的解为
,乙看错了方程组中的b,而得到方程组的解为 ,
,(1)甲把a看成了什么?乙把b看成了什么?
(2)求出原方程组的正确解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司试销一种成本为30元/件的新产品,按规定试销时的销售单价不低于成本单价,又不高于80元/件,试销中每天的销售量y(件)与销售单价x(元/件)满足下表中的函数关系.

(1)试求y与x之间的函数表达式;(2)设公司试销该产品每天获得的毛利润为S(元),求S与x之间的函数表达式(毛利润=销售总价-成本总价);
(2)当销售单价定为多少时,该公司试销这种产品每天获得的毛利润最大?
(3)最大毛利润是多少?此时每天的销售量是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】杭州休博会期间,嘉年华游乐场投资150万元引进一项大型游乐设施.若不计维修保养费用,预计开放后每月可创收33万元.而该游乐设施开放后,从第1个月到第x个月的维修保养费用累计为y(万元),且y=ax2+bx;若将创收扣除投资和维修保养费用称为游乐场的纯收益g(万元),g也是关于x的二次函数;
(1)若维修保养费用第1个月为2万元,第2个月为4万元.求y关于x的解析式;
(2)求纯收益g关于x的解析式;
(3)问设施开放几个月后,游乐场的纯收益达到最大;几个月后,能收回投资? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数y=-x2+bx+c的部分图象与x轴、y轴的交点分别为A(1,0),B(0,3),对称轴是x=-1,在下列结论中,错误的是( )
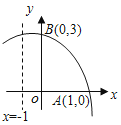
A.顶点坐标为(-1,4)
B.函数的解析式为y=-x2-2x+3
C.当x<0时,y随x的增大而增大
D.抛物线与x轴的另一个交点是(-3,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )

A.(-3,0)
B.(-2,0)
C.x=-3
D.x=-2
相关试题

