【题目】某班13位同学参加每周一次的卫生大扫除,按学校的卫生要求需要完成总面积为60m2的三个项目的任务,三个项目的面积比例和每人每分钟完成各项目的工作量如图所示: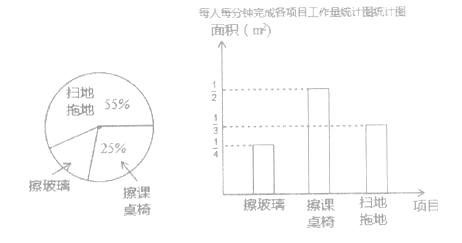
(1)从统计图中可知:擦玻璃的面积占总面积的百分比为 , 每人每分钟擦课桌椅
m2;
(2)扫地拖地的面积是m2;
(3)他们一起完成扫地和拖地任务后,把这13人分成两组,一组去擦玻璃,一组去擦课桌椅,如果你是卫生委员,该如何分配这两组的人数,才能最快地完成任务?(要有详细的解答过程)
参考答案:
【答案】
(1)20%;![]()
(2)33
(3)
解:设擦玻璃x人,则擦课桌椅(13-x)人,根据题意得:
( ![]() x):[
x):[ ![]() (13-x)]=20:25,
(13-x)]=20:25,
解得:x=8,
经检验x=8是原方程的解.
答:擦玻璃8人,擦课桌椅5人.
【解析】(1)根据题意得:
擦玻璃的面积占总面积的百分比是:1-55%-25%=20%;
每人每分钟擦课桌椅 ![]() m2;
m2;
故答案为:20%, ![]() ;
;
2)扫地拖地的面积是60×55%=33(m2);
故答案为:33.
(1)所有百分比的和为1;观察条形统计图可知;(2)总面积×所占百分比=扫地拖地面积;(3)使“擦玻璃”和“擦课桌椅”同时完成,则擦玻璃的人数×速度×时间:擦课桌椅的人数×速度×时间=20:25.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,AB=4,BC=5,点E在边CD上,以B为坐标原点,BA所在直线为y轴,BC所在直线为x轴,建立平面直角坐标系,A(0,4).以AE所在直线为折痕折叠长方形ABCD,点D恰好落在BC边上的F点.

(1)求点F的坐标;
(2)求点E的坐标;
(3)在AE上是否存在点P,使PB+PF最小?若存在,作出点P的位置,并求出PB+PF的最小值;不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】清清从家步行到公交车站台,等公交车去学校.下公交车后又步行了一段路程才到学校. 图中的折线表示清清的行程s(米)与所花时间t (分)之间的函数关系. 下列说法错误的是( )

A. 清清等公交车时间为3分钟 B. 清清步行的速度是80米/分
C. 公交车的速度是500米/分 D. 清清全程的平均速度为290米/分
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系xOy中,点A,B分别在x轴和y轴上,
 =
=  ,∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=
,∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=  的图象过点C,若以CD为边的正方形的面积等于
的图象过点C,若以CD为边的正方形的面积等于  ,则k的值是.
,则k的值是.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA,BC的平行线交于点E,且DE交AC于点O,连接AE.

(1)求证:四边形ADCE是菱形;
(2)若AC=2DE,求sin∠CDB的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是O的直径,点C在O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
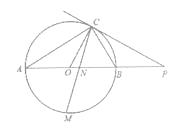
(1)求证:PC是O的切线;
(2)求证:BC= AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN·MC的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.

(1)求AD的长及抛物线的解析式;
(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动,设运动时间为t秒,当t为何值时,以P,Q,C为顶点的三角形与ADE相似?
(3)点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M,N,C,E为顶点的四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.
相关试题

