【题目】(1)方法回顾
在学习三角形中位线时,为了探索三角形中位线的性质,思路如下:
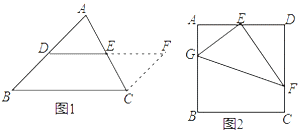
第一步添加辅助线:如图1,在△ABC中,延长DE (D、E分别是AB、AC的中点)到点F,使得EF=DE,连接CF;
第二步证明△ADE≌△CFE,再证四边形DBCF是平行四边形,从而得到DE∥BC,DE=![]() BC.
BC.
(2)问题解决
如图2,在正方形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若AG=2,DF=3,∠GEF=90°,求GF的长.
(3)拓展研究
如图3,在四边形ABCD中,∠A=100°,∠D=110°,E为AD的中点,G、F分别为AB、CD边上的点,若AG=4,DF=![]() ,∠GEF=90°,求GF的长.
,∠GEF=90°,求GF的长.

参考答案:
【答案】问题解决:GF=5;拓展研究:GF=![]() .
.
【解析】
(1)延长GE、FD交于点H,可证得△AEG≌△DEH,结合条件可证明EF垂直平分GH,可得GF=FH,可求得GF的长;
(2)过点D作AB的平行线交GE的延长线于点H,过H作CD的垂线,垂足为P,连接HF,可证明△AEG≌△DEH,结合条件可得到△HPD为等腰直角三角形,可求得PF的长,在Rt△HFP中,可求得HF,则可求得GF的长.
(1)如图2,延长GE、FD交于点H,
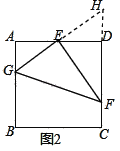
∵E为AD中点,
∴EA=ED,且∠A=∠EDH=90°,
在△AEG和△DEH中,
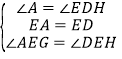
∴△AEG≌△DEH(ASA),
∴AG=HD=2,EG=EH,
∵∠GEF=90°,
∴EF垂直平分GH,
∴GF=HF=DH+DF=2+3=5;
(2)如图3,过点D作AB的平行线交GE的延长线于点H,过H作CD的垂线,垂足为P,连接HF,
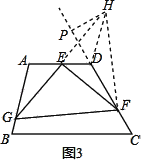
同(1)可知△AEG≌△DEH,GF=HF,
∴∠A=∠HDE=100°,AG=HD=4,
∵∠ADC=110°,
∴∠HDF=360°﹣100°﹣110°=150°,
∴∠HDP=30°,∴HP=2,
PD=PH=![]() ,
,
∴PF=PD+DF=![]()
在Rt△HFP中,∠HPF=90°,HP=2,PF=![]() ,
,
∴HF=![]() =
=![]() ,
,
∴GF=![]() .
.
-
科目: 来源: 题型:
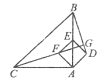
查看答案和解析>>【题目】如图,在RtΔABC中,AB=AC=4,∠BAC=900.点E为AB的中点,以AE为对角线作正方形ADEF,连接CF并延长交BD于点G,则线段CG的长等于________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=mx(m为常数)与双曲线y=
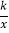 (k为常数)相交于A、B两点.
(k为常数)相交于A、B两点.(1)若点A的横坐标为3,点B的纵坐标为﹣4
①直接写出:k=____,m=____;
②点C在第一象限内是双曲线y=
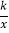 的点,当S△OAC=9时,求点C的坐标;
的点,当S△OAC=9时,求点C的坐标;(2)将直线y=mx向右平移得到直线y=mx+b,交双曲线y=
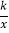 于点E(4,y1)和F(﹣2,y2),直接写出不等式mx2+bx<k的解集:_____.
于点E(4,y1)和F(﹣2,y2),直接写出不等式mx2+bx<k的解集:_____.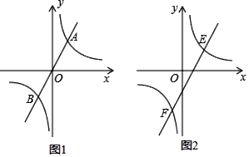
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年3月25日是全国中小学生安全教育日,某中学为加强学生的安全意识,组织了全校800名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分为100分)进行统计.请根据尚未完成的频率分布表和频数分布直方图解题.


(1)这次抽取了 名学生的竞赛成绩进行统计,其中:m= ,n=
(2)补全频数分布直方图.
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( )

A. 2 B.
 C.
C.  D. 2
D. 2
-
科目: 来源: 题型:
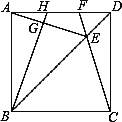
查看答案和解析>>【题目】如图,在正方形ABCD中,E是对角线BD上一点,且满足BE=BC.连接CE并延长交AD于点F,连接AE,过B点作BG⊥AE于点G,延长BG交AD于点H.在下列结论中:
①AH=DF; ②∠AEF=45°; ③S四边形EFHG=S△DEF+S△AGH,
其中正确的结论有_____________________.(填正确的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为300,测得大楼顶端 A的仰角为450(点B,C,E在同一水平直线上)。已知AB=50m,DE=10m,求障碍物B,C两点间的距离。(结果精确到1m,参考数据:
 )
)
相关试题

