【题目】2019年3月25日是全国中小学生安全教育日,某中学为加强学生的安全意识,组织了全校800名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分为100分)进行统计.请根据尚未完成的频率分布表和频数分布直方图解题.


(1)这次抽取了 名学生的竞赛成绩进行统计,其中:m= ,n=
(2)补全频数分布直方图.
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?
参考答案:
【答案】(1)200 m=70 n=0.12 ;(2)见解析 ;(3)224 .
【解析】
(1)用第一个分数段的频数除以它的频率可得到调查的总人数,然后用总人数乘以0.35得到m的值,用24除以总人数可得到n的值;
(2)利用80-90的频数为70可补全频数分布直方图;
(3)估计样本估计总体,用800乘以前面两分数段的频率之和可估计出该校安全意识不强的学生数.
解:(1)16÷0.08=200,
m=200×0.35=70,n=24÷200=0.12;
故答案为200,70;0.12;
(2)如图,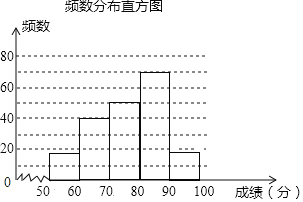
(3)800×(0.08+0.2)=224,
所以该校安全意识不强的学生约有224人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系xOy(如图)中,已知抛物线y=
 +bx+c点经过A(1,0)、B(0,2).
+bx+c点经过A(1,0)、B(0,2).(1)求该抛物线的表达式;
(2)设该抛物线的对称轴与x轴的交点为C,第四象限内的点D在该抛物线的对称轴上,如果以点A、C、D所组成的三角形与△AOB相似,求点D的坐标;
(3)设点E在该抛物线的对称轴上,它的纵坐标是1,联结AE、BE,求sin∠ABE.
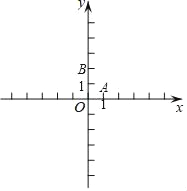
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个少年在绿茵场上游戏.小红从点A出发沿线段AB运动到点B,小兰从点C出发,以相同的速度沿⊙O逆时针运动一周回到点C,两人的运动路线如图1所示,其中AC
 DB.两人同时开始运动,直到都停止运动时游戏结束,其间他们与点C的距离y与时间x(单位:秒)的对应关系如图2所示.则下列说法正确的是( )
DB.两人同时开始运动,直到都停止运动时游戏结束,其间他们与点C的距离y与时间x(单位:秒)的对应关系如图2所示.则下列说法正确的是( )

A. 小红的运动路程比小兰的长
B. 两人分别在1.09秒和7.49秒的时刻相遇
C. 当小红运动到点D的时候,小兰已经经过了点D
D. 在4.84秒时,两人的距离正好等于⊙O的半径
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是“作一个30°角”的尺规作图过程.
已知:平面内一点A.
求作:∠A,使得∠A
 30°.
30°.作法:如图,
(1)作射线AB;
(2)在射线AB上取一点O,以O为圆心,OA为半径作圆,与射线AB相交于点C;
 (3)以C为圆心,OC为半径作弧,与⊙O交于点D,作射线AD.
(3)以C为圆心,OC为半径作弧,与⊙O交于点D,作射线AD.∠DAB即为所求的角.
请回答:该尺规作图的依据是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B
 90°,AB
90°,AB 4,BC
4,BC 2,以AC为边作△ACE,∠ACE
2,以AC为边作△ACE,∠ACE 90°,AC=CE,延长BC至点D,使CD
90°,AC=CE,延长BC至点D,使CD 5,连接DE.求证:△ABC∽△CED.
5,连接DE.求证:△ABC∽△CED.
-
科目: 来源: 题型:
查看答案和解析>>【题目】古代阿拉伯数学家泰比特·伊本·奎拉对勾股定理进行了推广研究:如图(图1中
 为锐角,图2中
为锐角,图2中 为直角,图3中
为直角,图3中 为钝角).
为钝角).
在△ABC的边BC上取
 ,
,  两点,使
两点,使 ,则
,则 ∽
∽ ∽
∽ ,
,  ,
,  ,进而可得
,进而可得
 ;(用
;(用 表示)
表示)若AB=4,AC=3,BC=6,则

 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数
 (x<0)与y=ax+b的图象交于点A(﹣1,n)和点B(﹣2,1).
(x<0)与y=ax+b的图象交于点A(﹣1,n)和点B(﹣2,1).(1)求k,a,b的值;
(2)直线x=m与
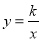 (x<0)的图象交于点P,与y=﹣x+1的图象交于点Q,当∠PAQ>90°时,直接写出m的取值范围.
(x<0)的图象交于点P,与y=﹣x+1的图象交于点Q,当∠PAQ>90°时,直接写出m的取值范围.
相关试题

