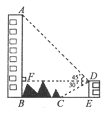
【题目】如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为300,测得大楼顶端 A的仰角为450(点B,C,E在同一水平直线上)。已知AB=50m,DE=10m,求障碍物B,C两点间的距离。(结果精确到1m,参考数据: ![]() )
)

参考答案:
【答案】障碍物B,C两点间的距离约为23 m
【解析】试题分析:过点D作DF⊥AB于点F,过点C作CH⊥DF于点H,则DE=BF=CH=20m,根据直角三角形的性质得出DF的长,在Rt△CDE中,利用锐角三角函数的定义得出CE的长,根据BC=BE-CE即可得出结论.
试题解析:
过点D作DF⊥AB交于AB于点F,则∠DFA=900,∠ADA=450,∠FDC=300,
∵AB⊥BE于点B,DE⊥BE于点E,
∴∠BFD=∠FBE=∠BED=900.
∴四边形BEDF是矩形
∴BF=DE,FD=BE,FD∥BE.
∵AB=50,DE=10,
∴AF=AB-BF=40
在RtΔAFD中, ![]() ,
,
∴DF=AF=40
∵FD∥BE,∴∠DCE=∠FDC=300.
在RtΔCDE中![]() ,
,
∴![]()
∴![]()
答:障碍物B,C两点间的距离约为23m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)方法回顾
在学习三角形中位线时,为了探索三角形中位线的性质,思路如下:
第一步添加辅助线:如图1,在△ABC中,延长DE (D、E分别是AB、AC的中点)到点F,使得EF=DE,连接CF;
第二步证明△ADE≌△CFE,再证四边形DBCF是平行四边形,从而得到DE∥BC,DE=
 BC.
BC.(2)问题解决
如图2,在正方形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若AG=2,DF=3,∠GEF=90°,求GF的长.
(3)拓展研究
如图3,在四边形ABCD中,∠A=100°,∠D=110°,E为AD的中点,G、F分别为AB、CD边上的点,若AG=4,DF=
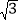 ,∠GEF=90°,求GF的长.
,∠GEF=90°,求GF的长.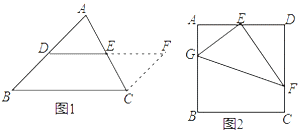

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( )

A. 2 B.
 C.
C.  D. 2
D. 2
-
科目: 来源: 题型:
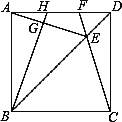
查看答案和解析>>【题目】如图,在正方形ABCD中,E是对角线BD上一点,且满足BE=BC.连接CE并延长交AD于点F,连接AE,过B点作BG⊥AE于点G,延长BG交AD于点H.在下列结论中:
①AH=DF; ②∠AEF=45°; ③S四边形EFHG=S△DEF+S△AGH,
其中正确的结论有_____________________.(填正确的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A,B在数轴上分别表示有理数a,b.A,B两点之间的距离表示为AB,在数轴上A,B两点之间的距离AB=|a﹣b|.利用数形结合思想回答下列问题:
(1)数轴上表示﹣2和8两点之间的距离是________.
(2)数轴上表示x和﹣4两点A和B之间的距离表示为__________;如果AB=2,那么x=___________.
(3)若点C表示的数为x,当点C在什么位置时,|
 x+1|+|
x+1|+| x1|取得的值最小,并直接写出最小值。
x1|取得的值最小,并直接写出最小值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB为⊙O的直径,BD和CD为⊙O的切线,切点分别为B和C.
(1)求证:AC∥OD;
(2)当BC=BD,且BD=6cm时,求图中阴影部分的面积(结果不取近似值).

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公园划船项目收费标准如下:

某班18名同学一起去该公园划船,若每人划船的时间均为1小时,则租船的总费用最低为________元.
相关试题

