【题目】已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.

(1)求证:EG=CG;
(2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论(均不要求证明).
参考答案:
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】
试题分析:(1)利用直角三角形斜边上的中线等于斜边的一半,可证出CG=EG.
(2)结论仍然成立,连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点;再证明△DAG≌△DCG,得出AG=CG;再证出△DMG≌△FNG,得到MG=NG;再证明△AMG≌△ENG,得出AG=EG;最后证出CG=EG.
(3)结论依然成立.还知道EG⊥CG.
(1)证明:∵四边形ABCD是正方形,
∴∠DCF=90°,
在Rt△FCD中,
∵G为DF的中点,
∴CG=![]() FD,
FD,
同理,在Rt△DEF中,
EG=![]() FD,
FD,
∴CG=EG.
(2)解:(1)中结论仍然成立,即EG=CG.
证法一:连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点.
在△DAG与△DCG中,
∵AD=CD,∠ADG=∠CDG,DG=DG,
∴△DAG≌△DCG(SAS),
∴AG=CG;
在△DMG与△FNG中,
∵∠DGM=∠FGN,FG=DG,∠MDG=∠NFG,
∴△DMG≌△FNG(ASA),
∴MG=NG;
∵∠EAM=∠AEN=∠AMN=90°,
∴四边形AENM是矩形,
在矩形AENM中,AM=EN,
在△AMG与△ENG中,
∵AM=EN,∠AMG=∠ENG,MG=NG,
∴△AMG≌△ENG(SAS),
∴AG=EG,
∴EG=CG.
证法二:延长CG至M,使MG=CG,
连接MF,ME,EC,
在△DCG与△FMG中,
∵FG=DG,∠MGF=∠CGD,MG=CG,
∴△DCG≌△FMG.
∴MF=CD,∠FMG=∠DCG,
∴MF∥CD∥AB,
∴EF⊥MF.
在Rt△MFE与Rt△CBE中,
∵MF=CB,∠MFE=∠EBC,EF=BE,
∴△MFE≌△CBE
∴∠MEF=∠CEB.
∴∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°,
∴△MEC为直角三角形.
∵MG=CG,
∴EG=![]() MC,
MC,
∴EG=CG.
(3)解:(1)中的结论仍然成立.理由如下:
过F作CD的平行线并延长CG交于M点,连接EM、EC,过F作FN垂直于AB于N.
由于G为FD中点,易证△CDG≌△MFG,得到CD=FM,
又因为BE=EF,易证∠EFM=∠EBC,则△EFM≌△EBC,∠FEM=∠BEC,EM=EC
∵∠FEC+∠BEC=90°,∴∠FEC+∠FEM=90°,即∠MEC=90°,
∴△MEC是等腰直角三角形,
∵G为CM中点,
∴EG=CG,EG⊥CG.



-
科目: 来源: 题型:
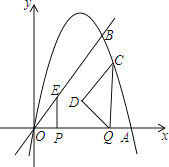
查看答案和解析>>【题目】如图,抛物线y=﹣x2+6x与x轴交于O,A两点,与直线y=2x交于O,B两点.点P在线段OA上以每秒1个单位的速度从点O向终点A运动,作EP⊥x轴交直线OB于E;同时在线段OA上有另一个动点Q,以每秒1个单位的速度从点A向点O运动(不与点O重合).作CQ⊥x轴交抛物线于点C,以线段CQ为斜边作如图所示的等腰直角△CQD.设运动时间为t秒.
(1)求点B的坐标;
(2)当t=1秒时,求CQ的长;
(3)求t为何值时,点E恰好落在△CQD的某一边所在的直线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校开展课外体育活动,决定开设A:篮球、B:乒乓球、C:踢毽子、D:跑步四种活动项目.为了解学生最喜欢哪一种活动项目(每人只选取一种),随机抽取了部分学生进行调查,并将调查结果绘成如甲、乙所示的统计图,请你结合图中信息解答下列问题.

(1)样本中最喜欢A项目的人数所占的百分比为 ,其所在扇形统计图中对应的圆心角度数是 度;
(2)请把条形统计图补充完整;
(3)若该校有学生1000人,请根据样本估计全校最喜欢踢毽子的学生人数约是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C.过点C作CD∥x轴,交抛物线的对称轴于点D.

(1)求该抛物线的解析式;
(2)若将该抛物线向下平移m个单位,使其顶点落在D点,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】绝对值大于1且小于5的所有的整数的和是___________;
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形从一个顶点最多能引出2015条对角线,这个多边形的边数是( )
A. 2015 B. 2016 C. 2017 D. 2018
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:4x2﹣4=_____.
相关试题

