【题目】如图1,等边△ABC边长为6,AD是△ABC的中线,P为线段AD(不包括端点A、D)上一动点,以CP为一边且在CP左下方作如图所示的等边△CPE,连结BE. 
(1)点P在运动过程中,线段BE与AP始终相等吗?说说你的理由;
(2)若延长BE至F,使得CF=CE=5,如图2,问: ①求出此时AP的长;
②当点P在线段AD的延长线上时,判断EF的长是否为定值,若是请直接写出EF的长;若不是请简单说明理由.
参考答案:
【答案】
(1)解:BE=AP.
理由:∵△ABC和△CPE均为等边三角形,
∴∠ACB=∠PCE=60°,AC=BC,CP=CE.
∵∠ACP+∠DCP=∠DCE+∠PCD=60°,
∴∠ACP=∠BCE.
∵在△ACP和△BCE中, 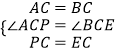 ,
,
∴△ACP≌△BCE.
∴BE=AP
(2)解:①如图2所示:过点C作CH⊥BE,垂足为H.
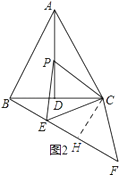
∵AB=AC,AD是BC的中点,
∴∠CAD=∠BAD= ![]() ∠BAC=30°.
∠BAC=30°.
∵由(1)可知:△ACP≌△BCE,
∴∠CBE=∠CAD=30°,AP=BE.
∵在Rt△BCH中,∠HBC=30°,
∴HC= ![]() BC=3,NH=
BC=3,NH= ![]() BC=3
BC=3 ![]() .
.
∵在Rt△CEH中,EC=5,CH=3,
∴EH= ![]() =4.
=4.
∴BE=HB﹣EH=3 ![]() ﹣4.
﹣4.
∴AP=3 ![]() ﹣4.
﹣4.
②如图3所示:过点C作CH⊥BE,垂足为H.
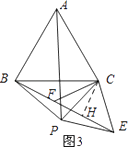
∵△ABC和△CEP均为等边三角形,
∴AC=BC,CE=PC,∠ACB=∠ECP.
∴∠ACB+∠BCP=∠ECP+BCP,即∠BCE=∠ACP.
∵在△ACP和△BCE中, 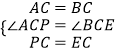 ,
,
∴△ACP≌△BCE.
∴∠CBH=∠CAP=30°.
∵在Rt△BCH中,∠CBH=30°,
∴HC= ![]() BC=3.
BC=3.
∵FC=CE,CH⊥FE,
∴FH=EH.
∴FH=EH= ![]() =4.
=4.
∴EF=FH+EH=4+4=8
【解析】(1)先证明∠ACP=∠BCE,然后依据SAS证明△ACP≌△BCE,由全等三角形的性质可得到BE=AP;(2)过点C作CH⊥BE,垂足为H,先依据等腰三角形三线合一的性质求得∠CAD=30°,然后由△ACP≌△BCE可求得∠CBH=30°,依据含30°直角三角形的性质可求得CH的长,从而可求得BH的长,然后在△ECH中依据勾股定理可求得EH的长,故此可求得BE的长,最后根据AP=BE求解即可;(3)首先根据题意画出图形,过点C作CH⊥BE,垂足为H.先证△ACP≌△BCE,从而得到∠CBH=30°,由含30°直角三角形的性质可求得CH的长,依据勾股定理可求得FH的长,然后由等腰三角形三线合一的性质可得到HE=FH,故此可求得EF的长.
【考点精析】掌握等边三角形的性质是解答本题的根本,需要知道等边三角形的三个角都相等并且每个角都是60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xoy中,抛物线
 与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,直线l经过点A和点C,连接BC.将直线l沿着x轴正方形平移m个单位
与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,直线l经过点A和点C,连接BC.将直线l沿着x轴正方形平移m个单位 得到直线
得到直线 ,
,  交
交 轴于点D,交BC于点E,交抛物线于点F.
轴于点D,交BC于点E,交抛物线于点F.(1)求点
 ,点
,点 和点
和点 的坐标
的坐标(2)如图2,将
 沿直线
沿直线 翻折得到
翻折得到 ,求点
,求点 的坐标(用含
的坐标(用含 的代数式表示);
的代数式表示);(3)在(2)的条件下,当点
 落在直线
落在直线 上时,请直接写出点
上时,请直接写出点 的坐标
的坐标
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣22×7﹣(﹣3)×6+5;
(2)( ﹣
﹣  ﹣
﹣ 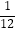 )×24÷(﹣2);
)×24÷(﹣2);
(3)56×1 +56×(﹣
+56×(﹣  )﹣56×
)﹣56×  ;
;
(4)(﹣1)4﹣ ×[2﹣(﹣3)2].
×[2﹣(﹣3)2]. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.

(1)出发2秒后,求PQ的长;
(2)从出发几秒钟后,△PQB第一次能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式计算正确的是( )
A.6a+a=6a2
B.﹣2a+5b=3ab
C.4m2n﹣2mn2=2mn
D.3ab2﹣5b2a=﹣2ab2 -
科目: 来源: 题型:
查看答案和解析>>【题目】现今世界上较先进的计算机显卡每秒可绘制出27000000个三角形,且显示逼真,用科学记数法表示这种显卡每秒绘制出三角形个数( )
A.27×106
B.0.27×108
C.2.7×107
D.270×105 -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:a是不为1的有理数,我们把
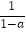 称为a的差倒数.
称为a的差倒数.
如:2的差倒数是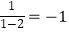 ,﹣1的差倒数是
,﹣1的差倒数是 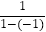 =
=  .
.
已知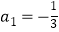 ,
,
(1)a2是a1的差倒数,则a2=
(2)a3是a2的差倒数,则a3=
(3)a4是a3的差倒数,则a4= ,…,依此类推,则a2009=
相关试题

