【题目】如图,在平面直角坐标系中,每个小正方形的边长为一个单位长度.已知△ABC的顶点A(-2,5)、B(-4,1)、C(2,3),将△ABC平移得到△A′B′C′,点A(a,b)对应点A′(a+3,b-4)
(1) 画出△A′B′C′并写出点B′、C′的坐标
(2) 试求线段AB在整个平移的过程中在坐标平面上扫过的面积
(3) 在x轴上存在一点P,使得S△ABP=6,则点P的坐标是_____________.

参考答案:
【答案】(1)B'(-1,-3),C'(5,-1);(2)20;(3)(![]() ,0)或(
,0)或(![]() ,0).
,0).
【解析】
(1)根据横坐标+3是向右平移3个单位长度,纵坐标-4是向下平移4个单位长度,画出图形即可;(2)如图:图中阴影面积即线段AB扫过的面积,根据平行四边形面积公式计算即可;(3)过点B作BD⊥x轴于D,过点A作AE⊥x轴于E,可求出梯形AEDB的面积为6,可知P点在D点左侧或在E点右侧,分情况通过梯形和三角形的面积的和与差列方程求出x值即可;
(1)如图:三角形A′B′C′即为所求; B′(-1,-3)、C′(5,-1),设P点坐标为(x,0),
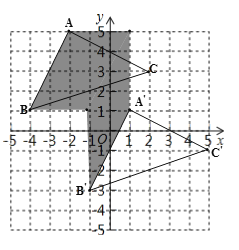
(2) S=3×4+4×2=20;
(3) 过点B作BD⊥x轴于D,过点A作AE⊥x轴于E,设P点坐标为(x,0),
∴S梯形AEDB=![]()
∴P点在D点左侧或E点右侧,
① 当P在E点右侧时,S△ABP=6+![]() ·(x+2)·5-
·(x+2)·5-![]() ·(x+4)·1=6,解得
·(x+4)·1=6,解得![]()
② 当P在D点左侧时,S△ABP=![]() ·(-x-2)·5-6-
·(-x-2)·5-6-![]() ·(-x-4)·1=6,解得
·(-x-4)·1=6,解得![]()
∴P(![]() ,0)或(
,0)或(![]() ,0),
,0),
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,则∠A、∠C、∠E、∠F满足的数量关系是( )

A. ∠A=∠C+∠E+∠F B. ∠A+∠E﹣∠C﹣∠F=180°
C. ∠A﹣∠E+∠C+∠F=90° D. ∠A+∠E+∠C+∠F=360°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲、乙两人到距离A地35千米的B地办事,甲步行先走,乙骑车后走,两人行进的路程和时间的关系如图所示,根据图示提供的信息解答:
(1)乙比甲晚 小时出发;乙出发 小时后追上甲;
(2)求乙比甲早几小时到达B地?

-
科目: 来源: 题型:
查看答案和解析>>【题目】商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同.
(1)若他去买一瓶饮料,则他买到奶汁的概率是;
(2)若他两次去买饮料,每次买一瓶,且两次所买饮料品种不同,请用树状图或列表法求出他恰好买到雪碧和奶油的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线AB平移至△FEG,DE、FG相交于点H.
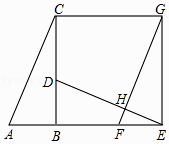
(1)判断线段DE、FG的位置关系,并说明理由;
(2)连结CG,求证:四边形CBEG是正方形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E、F两点,连结DE,已知∠B=30°,⊙O的半径为6,弧DE的长度为2π.

(1)求证:DE∥BC;
(2)若AF=CE,求线段BC的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】为节约用水、保护水资源,本市制定了一套节约用水的管理措施,其中规定每月用水量超过m(吨)时,超过部分每吨加收环境保护费
 元.下图反映了每月收取的水费y(元)与每月用水量x(吨)之间的函数关系的图象.按上述方案,一家酒店四、五两月用水量及缴费情况如表:
元.下图反映了每月收取的水费y(元)与每月用水量x(吨)之间的函数关系的图象.按上述方案,一家酒店四、五两月用水量及缴费情况如表: 月份
用水量x(吨)
水费y(元)
四月
35
59.5
五月
80
151

(1)求出m的值;
(2)写出y与x之间的函数关系式,并指出自变量x的取值范围.
相关试题

