【题目】如图所示已知![]() ,
,![]() ,OM平分
,OM平分![]() ,ON平分
,ON平分![]() ;
;
(1)![]() ;
;
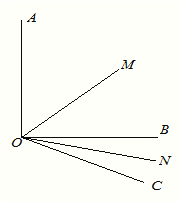
(2)如图∠AOB=900,将OC绕O点向下旋转,使∠BOC=![]() ,仍然分别作∠AOC,∠BOC的平分线OM,ON,能否求出∠MON的度数,若能,求出其值,若不能,试说明理由.
,仍然分别作∠AOC,∠BOC的平分线OM,ON,能否求出∠MON的度数,若能,求出其值,若不能,试说明理由.

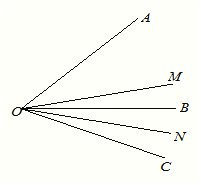
(3)![]() ,
,![]() ,仍然分别作∠AOC,∠BOC的平分线OM,ON,能否求出∠MON的度数,若能,求
,仍然分别作∠AOC,∠BOC的平分线OM,ON,能否求出∠MON的度数,若能,求![]() 的度数;并从你的求解中看出什么什么规律吗?
的度数;并从你的求解中看出什么什么规律吗?
参考答案:
【答案】(1)![]() ;
;
(2)能,因为∠AOB=900,∠BOC=![]() , 所以∠AOC=900+
, 所以∠AOC=900+![]() ,
,
因为OM、 ON平分∠AOC,∠BOC的线
所以∠MOC=![]() ∠AOC=
∠AOC=![]() (900+
(900+![]() )=450+x
)=450+x
所以∠CON=![]() ∠BOC=x
∠BOC=x
所以∠MON=∠MOC-∠CON=450+x-x=450
(3)能,因为∠AOB=![]() ,∠BOC=
,∠BOC=![]() ,
,
所以∠AOC=![]() +
+![]() ,
,
因为OM、 ON平分∠AOC,∠BOC的线
所以∠MOC=![]() ∠AOC=
∠AOC=![]() (
(![]() +
+![]() )
)
所以∠CON=![]() ∠BOC=
∠BOC=![]()
![]()
所以∠MON=∠MOC-∠CON=![]() (
(![]() +
+![]() )-
)-![]()
![]() =
=![]()
![]()
即![]() .
.
【解析】
(1)根据题意可知,∠AOC=120°,由OM平分∠AOC,ON平分∠BOC;推出∠MOC=∠AOC=60°,∠CON=![]() ∠BOC=15°,由图形可知,∠MON=∠MOC-∠CON,即∠MON=45°;(2)根据(1)的求解思路,先利用角平分线的定义表示出∠MOC与∠NOC的度数,然后相减即可得到∠MON的度数;(3)用α、β表示∠MOC,∠NOC,根据∠MON=∠MOC-∠NOC得到.
∠BOC=15°,由图形可知,∠MON=∠MOC-∠CON,即∠MON=45°;(2)根据(1)的求解思路,先利用角平分线的定义表示出∠MOC与∠NOC的度数,然后相减即可得到∠MON的度数;(3)用α、β表示∠MOC,∠NOC,根据∠MON=∠MOC-∠NOC得到.
(1)(1)∵∠AOB=90°,∠BOC=30°,
∴∠AOC=∠AOB+∠BOC=90°+30°=120°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=∠AOC=60°,∠CON=![]() ∠BOC=15°,
∠BOC=15°,
∴∠MON=∠MOC-∠CON=60°-15°=45°;
故答案为:45;
(2)能.∵∠AOB=90°,∠BOC=2x°,
∴∠AOC=90°+2x°,
∵OM、ON分别平分∠AOC,∠BOC,
∴∠MOC=![]() ∠AOC=
∠AOC=![]() (90°+2x°)=45°+x,
(90°+2x°)=45°+x,
∴∠CON=![]() ∠BOC=x,
∠BOC=x,
∴∠MON=∠MOC-∠CON=45°+x-x=45°
(3))∵∠AOB=α,∠BOC=β,
∴∠AOC=∠AOB+∠BOC=α+β,
∵OM平分∠AOC,
∴∠MOC=![]() ∠AOC=
∠AOC=![]() (α+β),
(α+β),
∵ON平分∠BOC,
∴∠NOC=![]() ∠BOC=
∠BOC=![]() ,
,
∴∠MON=∠MOC-∠NOC=![]() (α+β)-
(α+β)-![]() =
=![]() .
.
-
科目: 来源: 题型:
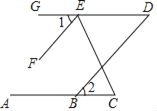
查看答案和解析>>【题目】如图,已知∠1=∠2=50°,EF∥DB.
(1)DG与AB平行吗?请说明理由.
(2)若EC平分∠FED,求∠C的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,BC=2,将矩形ABCD绕点D顺时针旋转90°,点A,C分别落在点A′、C′处,并且点A′,C′,B在同一条直线上,则tan∠ABA′的值为 .
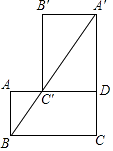
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有甲、乙两个瓷器店出售茶壶和茶杯,茶壶每只价格为20元,茶杯每只价格为5元,已知甲店制定的优惠方法是买一只茶壶送一只茶杯,乙店按总价的92%付款.学校办公室需要购买茶壶4只,茶杯若干只(不少于4只).
(1)当购买多少只茶杯时,两店的优惠方法付款一样多?
(2)当需要购买40只茶杯时,若让你去办这件事,你打算去哪家商店购买?为什么?
-
科目: 来源: 题型:
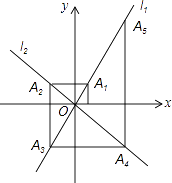
查看答案和解析>>【题目】如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1 , l2 , 过点(1,0)作x轴的垂线交l1于点A1 , 过点A1作y轴的垂线交l2于点A2 , 过点A2作x轴的垂线交l1于点A3 , 过点A3作y轴的垂线交l2于点A4 , …依次进行下去,则点A2017的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B的坐标为(18,6).
(1)求直线l1,l2对应的函数表达式;
(2)点C为线段OB上一动点(点C不与点O,B重合),作CD∥y轴交直线l2于点D,设点C的纵坐标为a,求点D的坐标(用含a的代数式表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:线段AB=20cm.
(1)如图1:点P沿线段AB自A点向B点以2厘米/秒运动,点P出发2秒后,点Q沿线段BA自B点向A点以3厘米/秒运动,问再经过几秒后P、Q相距5cm?

(2)如图2:
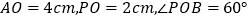 ,点P绕着点O以60度/秒的速度逆时针旋转一周停止,同时点Q沿直线BA自B点向A点运动,假若点P、Q两点能相遇,求点Q运动的速度 .
,点P绕着点O以60度/秒的速度逆时针旋转一周停止,同时点Q沿直线BA自B点向A点运动,假若点P、Q两点能相遇,求点Q运动的速度 . 
相关试题

