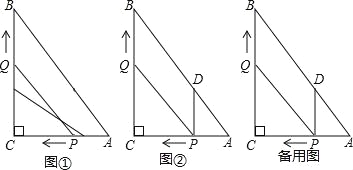
【题目】如图①，在Rt△ABC中，∠C=90°，AC=6，BC=8，动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动，动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动，点P，Q分别从点A、C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t妙（t≥0）．

（1）若三角形CPQ是等腰三角形，求t的值．

（2）如图②，过点P作PD∥BC，交AB于点D，连接PQ；

①是否存在t的值，使四边形PDBQ为菱形？若存在，求出t的值；若不存在，说明理由，并探究如何改变点Q的速度（匀速运动），使四边形PDBQ在某一时刻为菱形，求点Q的速度．

②当t取何值时，△CPQ的外接圆面积的最小？并且说明此时△CPQ的外接圆与直线AB的位置关系？

参考答案：

【答案】（1）2（2）①不存在，②t=时，PQ最小值为，△CPQ的外接圆与直线AB相交

【解析】

试题分析：（1）根据CQ=CP，列出方程即可解决．

（2））①不存在．不妨设四边形PDBQ是菱形，推出矛盾即可．

②如图，⊙O是△PQC的外接圆的圆心，作OM⊥AB于M，OE⊥AC于E，OF⊥BC于F，连接OB、OC、OA，由ACOF+ACOE+ABOM=BCAC求出OM以及圆的半径即可解决问题．

试题解析：（1）∵△CBP是等腰三角形，∠C=90°，

∴CQ=CP，

∴6﹣t=2t，

∴t=2，

∴t=2秒时，△CBP是等腰三角形．

（2）①不存在．

理由：不妨设四边形PDBQ是菱形，

则PD=BQ，

∴t=8﹣2t，

∴t=，

∴CQ=，PC=6﹣=，BQ=PD=，

∴OQ==6，

∴PQ≠BQ，

∴假设不成立，

∴不存在．

设点Q的速度为每秒a个单位长度．

∵四边形PDBQ是菱形，

∴PD=BD，

∴t=10﹣t，

∴t=，

∴BQ=PD=，

∴6﹣a=，

∴a=．

∴点Q的速度为每秒个长度单位时，使四边形PDBQ在某一时刻为菱形．

②如图，⊙O是△PQC的外接圆的圆心，作OM⊥AB于M，OE⊥AC于E，OF⊥BC于F，连接OB、OC、OA．

∵PQ===，

∴t=时，PQ最小值为．

此时PC=，CQ=，PQ=，

∵ACOF+ACOE+ABOM=BCAC，

∴×8×+×6×+×10×OM=24，

∴OM=，

∴OM＜OP，

∴△CPQ的外接圆与直线AB相交．

关闭