【题目】材料阅读:对于一个圆和一个正方形给出如下定义:若圆上存在到此正方形四条边距离都相等的点,则称这个圆是该正方形的“等距圆”.
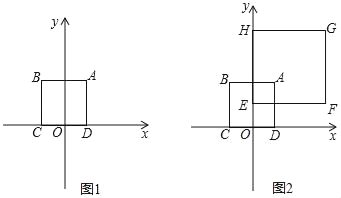
如图1,在平面直角坐标系xOy中,正方形ABCD的顶点A的坐标为(2,4),顶点C、D在x轴上,且点C在点D的左侧.
(1)当r=2![]() 时,在P1(2,0),P2(﹣4,2),P3(2
时,在P1(2,0),P2(﹣4,2),P3(2![]() ,2),P4(2﹣2
,2),P4(2﹣2![]() ,0)中可以成为正方形ABCD的“等距圆”的圆心的是 ;
,0)中可以成为正方形ABCD的“等距圆”的圆心的是 ;
(2)若点P坐标为(﹣2,﹣1),则当⊙P的半径r= 时,⊙P是正方形ABCD的“等距圆”.试判断此时⊙P与直线BD的位置关系?并说明理由.
(3)如图2,在正方形ABCD所在平面直角坐标系xOy中,正方形EFGH的顶点F的坐标为(8,2),顶点E、H在y轴上,且点H在点E的上方.若⊙P同时为上述两个正方形的“等距圆”,且与BC所在直线相切,求⊙P的圆心P的坐标.
参考答案:
【答案】(1) P1(2,0),P2(﹣2,4)或P4(0,2﹣2![]() );(2)
);(2)![]() 相交;(3) (
相交;(3) (![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】分析:(1)根据“等距圆”的定义,可知只要圆经过正方形的中心,即是正方形的“等距圆”,也就是说圆心与正方形中心的距离等于圆的半径即可,从而可以判断哪个点可以成为正方形ABCD的“等距圆”的圆心,本题得以解决;
(2)根据题意可知,只要求出点P与正方形ABCD的中心的距离即可求得半径r的长度,连接PE,可以得到直线PE的解析式,看点B是否在此直线上,由BE与直线AC的关心可以判断PE与直线AC的关系,本题得以解决;
(3)根据题意,可以得到点P满足的条件,列出形应的二元一次方程组,从而可以求得点P的坐标.
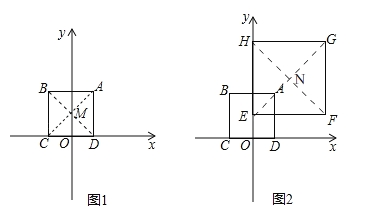
详解:(1)连接AC、BD相交于点M,如右图1所示.
∵四边形ABCD是正方形,∴点M是正方形ABCD的中心,到四边的距离相等,∴⊙P一定过点M.
∵正方形ABCD的顶点A的坐标为(2,4),顶点C、D在x轴上,且点C在点D的左侧,∴点M(0,2),设⊙P的圆心坐标是(x,y),∴(x﹣0)2+(y﹣2)2=(2 ![]() )2,将P1(2,0),P2(﹣4,2),P3(2
)2,将P1(2,0),P2(﹣4,2),P3(2![]() ,2),P4(2﹣2
,2),P4(2﹣2![]() ,0)分别代入上面的方程,只有P1(2,0),P2(﹣2,4)和P4(0,2﹣2
,0)分别代入上面的方程,只有P1(2,0),P2(﹣2,4)和P4(0,2﹣2![]() )成立.
)成立.
故答案为:P1(2,0),P2(﹣2,4)或P4(0,2﹣2![]() );
);
(2)由题意可得: 点M的坐标为(0,2),点P(﹣2,﹣1),∴r=![]() =
=![]() ,即当P点坐标为(﹣2,﹣1),则当⊙P的半径r是
,即当P点坐标为(﹣2,﹣1),则当⊙P的半径r是![]() 时,⊙P是正方形ABCD的“等距圆”;
时,⊙P是正方形ABCD的“等距圆”;
故答案为:![]() .
.
此时⊙P与直线AC的位置关系是相交,理由:∵正方形ABCD的顶点A的坐标为(2,4),顶点C、D在x轴上,且点C在点D的左侧,∴点B(﹣2,4),D(2,0),设过点B(﹣2,4),点D(2,0)的直线的解析式为y=kx+b,则 ![]() ,解得:
,解得:![]() ,即直线AC的解析式为:y=﹣x+2①,∴过点P(﹣2,﹣1)垂直于BD的直线解析式为y=x+1②,记垂足为G,联立①②,解得:G的坐标为(
,即直线AC的解析式为:y=﹣x+2①,∴过点P(﹣2,﹣1)垂直于BD的直线解析式为y=x+1②,记垂足为G,联立①②,解得:G的坐标为(![]() ),∴PG=
),∴PG=![]()
∴点P(﹣2,﹣1)到直线BD的距离为:![]() <
<![]() ;
;
∴此时⊙P与直线AC的位置关系是相交;
(3)设点P的坐标为(x,y),连接HF、EG交于点N,则点N为正方形EFGH的中心,其坐标为(4,6)如图2所示.
∵点E(0,2),N(4,6),点C(﹣2,0),点B(﹣2,4),⊙P同时为上述两个正方形的“等距圆”,且与BC所在直线相切,∴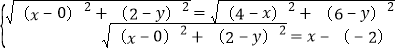 ,
,
解得:![]() 或
或![]()
即⊙P的圆心P的坐标是(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】请阅读下列材料:
问题:如图1,在等边三角形ABC内有一点P,且PA=2,PB=
 ,PC=1、求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1、求∠BPC度数的大小和等边三角形ABC的边长.李明同学的思路是:将△BPC绕点B逆时针旋转60°,画出旋转后的图形(如图2),连接PP′,可得△P′PC是等边三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可证),从而得到∠BPC=∠AP′B=__________;,进而求出等边△ABC的边长为__________;
问题得到解决.
请你参考李明同学的思路,探究并解决下列问题:如图3,在正方形ABCD内有一点P,且PA=
 ,BP=
,BP= ,PC=1.求∠BPC度数的大小和正方形ABCD的边长.
,PC=1.求∠BPC度数的大小和正方形ABCD的边长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为奖励学习之星,准备在某商店购买A、B两种文具作为奖品,已知一件A种文具的价格比一件B种文具的价格便宜5元,且用600元买A种文具的件数是用400元买B种文具的件数的2倍.
(1)求一件A种文具的价格;
(2)根据需要,该校准备在该商店购买A、B两种文具共150件.
①求购买A、B两种文具所需经费W与购买A种文具的件数a之间的函数关系式;
②若购买A种文具的件数不多于B种文具件数的2倍,且计划经费不超过2750元,求有几种购买方案,并找出经费最少的方案,及最少需要多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,-3),动点P在抛物线上.
(1)b =_________,c =_________,点B的坐标为_____________;(直接填写结果)
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】莒南县欲从某师范院校招聘一名“特岗教师”,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如表:
候选人
甲
乙
丙
丁
测试成绩
面试
86
91
90
83
笔试
90
83
83
92
根据录用程序,作为人民教师面试的成绩应该比笔试的成绩更重要,并分别赋予它们6和4的权.根据四人各自的平均成绩,你认为将录取( )
A.甲B.乙C.丙D.丁
-
科目: 来源: 题型:
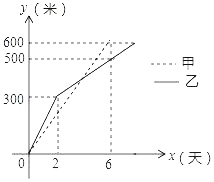
查看答案和解析>>【题目】甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(单位:米)与挖掘时间x(单位:天)之间的关系如图所示,则下列说法中:①甲队每天挖100米;②乙队开挖两天后,每天挖50米;③当x=4时,甲、乙两队所挖管道长度相同;④甲队比乙队提前2天完成任务.正确的是_____(直接填序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】作图与探究:
如图,已知点A、O、B是正方形网格的格点(网格线的交点),点P是∠AOB的边0B上的一点.
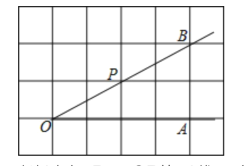
(1)过点P画OB的垂线,交OA于点E;
(2)过点P画OA的垂线,垂足为H;
(3)过点P画OA的平行线PC;
(4)若每个小正方形的边长是1,则点P到OA的距离是_________;
(5)线段PE、PH、OE的大小关系是___________(用“<"连接).
相关试题

