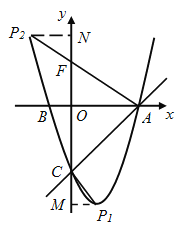
【题目】如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,-3),动点P在抛物线上.
(1)b =_________,c =_________,点B的坐标为_____________;(直接填写结果)
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.

参考答案:
【答案】(1)![]() ,
, ![]() ,
, ![]() (2)存在P的坐标是
(2)存在P的坐标是![]() 或
或![]() (3)当EF最短时,点P的坐标是:(
(3)当EF最短时,点P的坐标是:(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() )
)
【解析】试题分析:(1)根据题意得出答案;(2)分以点C为直角顶点和点A为直角顶点两种情况分别进行计算;两种情况都根据等腰直角三角形的性质得出点的坐标;(3)根据垂线段最短,可得当OD⊥AC时,OD最短,即EF最短,根据OC=OA=3,OD⊥AC得出 D是AC的中点,从而得出点P的纵坐标,然后根据题意得出方程,从而求出点P的坐标.
试题解析:(1)![]() ,
,![]() , (-1,0).
, (-1,0).
(2)存在.
第一种情况,当以C为直角顶点时,过点C作CP1⊥AC,交抛物线于点P1.过点P1作y轴的垂线,垂足是M.
∵OA=OC,∠AOC =90° ∴∠OCA=∠OAC=45°. ∵∠ACP1=90°, ∴∠MCP1=90°-45°=45°=∠C P1M.
∴MC=MP1. 由(1)可得抛物线为![]() .
.
设![]() ,则
,则![]() , 解得:
, 解得:![]() (舍去),
(舍去),![]() .
.
∴![]() . 则P1的坐标是
. 则P1的坐标是![]() .
.
第二种情况,当以A为直角顶点时,过点A作AP2⊥AC,交抛物线于点P2,过点P2作y轴的垂线,垂足是N,AP2交y轴于点F. ∴P2N∥x轴.由∠CAO=45°, ∴∠OAP2=45°. ∴∠FP2N=45°,AO=OF=3.
∴P2N=NF. 设![]() ,则
,则![]() . 解得:
. 解得:![]() (舍去),
(舍去),![]() .
.
∴![]() , 则P2的坐标是
, 则P2的坐标是![]() .
.
综上所述,P的坐标是![]() 或
或![]()
(3)连接OD,由题意可知,四边形OFDE是矩形,则OD=EF.
根据垂线段最短,可得当OD⊥AC时,OD最短,即EF最短. 由(1)可知,在Rt△AOC中,
∵OC=OA=3,OD⊥AC, ∴ D是AC的中点. 又∵DF∥OC, ∴![]() .
.
∴点P的纵坐标是![]() 则
则![]() , 解得:
, 解得:![]() .
.
∴当EF最短时,点P的坐标是:(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△AOB中,AB⊥OB,且AB=OB=3,设直线
 截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )
截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若AC=6,BC=8,OA=2,求线段DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】请阅读下列材料:
问题:如图1,在等边三角形ABC内有一点P,且PA=2,PB=
 ,PC=1、求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1、求∠BPC度数的大小和等边三角形ABC的边长.李明同学的思路是:将△BPC绕点B逆时针旋转60°,画出旋转后的图形(如图2),连接PP′,可得△P′PC是等边三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可证),从而得到∠BPC=∠AP′B=__________;,进而求出等边△ABC的边长为__________;
问题得到解决.
请你参考李明同学的思路,探究并解决下列问题:如图3,在正方形ABCD内有一点P,且PA=
 ,BP=
,BP= ,PC=1.求∠BPC度数的大小和正方形ABCD的边长.
,PC=1.求∠BPC度数的大小和正方形ABCD的边长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列已知条件,能唯一画出△ABC的是( )
A. AB=5,BC=3,AC=8 B. AB=4,BC=3,∠A=30°
C. ∠C=90°,AB=6 D. ∠A=60°,∠B=45°,AB=4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,转盘A的三个扇形面积相等,分别标有数字1,2,3,转盘B的四个扇形面积相等,分别有数字1,2,3,4.转动A、B转盘各一次,当转盘停止转动时,将指针所落扇形中的两个数字相乘(当指针落在四个扇形的交线上时,重新转动转盘).
(1)用树状图或列表法列出所有可能出现的结果;
(2)求两个数字的积为奇数的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,直径AB⊥CD,垂足为E,点M在OC上,AM的延长线交⊙O于点G,交过C的直线于F,∠1=∠2,连结CB与DG交于点N.
(1)求证:CF是⊙O的切线;
(2)求证:△ACM∽△DCN;
(3)若点M是CO的中点,⊙O的半径为4,cos∠BOC=
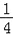 ,求BN的长.
,求BN的长.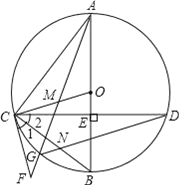
相关试题

