Question

【题目】如图，有一个边长不定的正方形，它的两个相对的顶点分别在边长为1的正六边形一组平行的对边上，另外两个顶点在正六边形内部（包括边界），则正方形边长的取值范围是 ．

Answer 1

【答案】（ ）

【解析】

试题分析：因为AC为对角线，故当AC最小时，正方形边长此时最小.

①当 A、C都在对边中点时（如下图所示位置时），显然AC取得最小值，

∵正六边形的边长为1，

∴AC=,

∴a2+a2=AC2=.

∴a==.

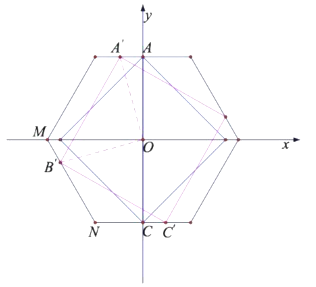
②当正方形四个顶点都在正六边形的边上时，a最大（如下图所示）.

设A′（t,）时，正方形边长最大.

∵OB′⊥OA′.

∴B′（-，t）

设直线MN解析式为：y=kx+b,M（-1，0），N（-， -）（如下图）

∴.

∴.

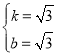∴直线MN的解析式为：y=（x+1）,

将B′（-， t）代入得：t=-.

此时正方形边长为A′B′取最大.

∴a==3-.

故答案为：.