【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
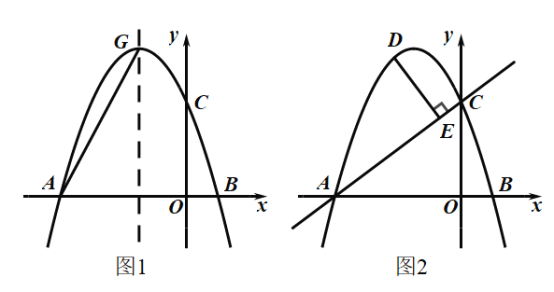
(1)求抛物线的解析式;
(2)如图1,抛物线的对称轴交抛物线于点![]() ,在
,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 的周长最小?若存在,求出点
的周长最小?若存在,求出点![]() 坐标;若不存在,请说明理由;
坐标;若不存在,请说明理由;
(3)如图2,点![]() 为直线
为直线![]() 上方抛物线上的动点,
上方抛物线上的动点,![]() 于点
于点![]() ,求线段
,求线段![]() 的最大值.
的最大值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由题意利用待定系数法将![]() ,
,![]() 代入
代入![]() 求解即可;
求解即可;
(2)根据题意作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连接
,连接![]() ,交
,交![]() 轴于点
轴于点![]() ,此时
,此时![]() 的周长最小,并设直线
的周长最小,并设直线![]() 的解析式为
的解析式为![]() ,将
,将![]() ,
,![]() 代入
代入![]() ,进行分析运算求解即可;
,进行分析运算求解即可;
(3)根据题意过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 交
交![]() 于点
于点![]() ,进而求出点
,进而求出点![]() 的坐标并设直线
的坐标并设直线![]() 的解析式为
的解析式为![]() ,将
,将![]() ,
,![]() 代入
代入![]() 进行运算以及设平行于
进行运算以及设平行于![]() 的直线为
的直线为![]() 进行分析运算.
进行分析运算.
解:(1)将![]() ,
,![]() 代入
代入![]() 得,
得, 解得,
解得,
∴抛物线的解析式为![]() .
.
(2)作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连接
,连接![]() ,交
,交![]() 轴于点
轴于点![]() ,此时
,此时![]() 的周长最小.
的周长最小.

![]()
![]()
![]()
设直线![]() 的解析式为
的解析式为![]() ,将
,将![]() ,
,![]()
代入![]() ,得
,得 ,
,
解得 ,
,
∴直线![]() 的解析式为
的解析式为![]()
当![]() 时,
时,![]()
∴点![]() 的坐标为
的坐标为![]() .
.
(3)如图,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 交
交![]() 于点
于点![]() .
.

当![]() 时,
时,![]()
∴点![]() 的坐标为
的坐标为![]()
设直线![]() 的解析式为
的解析式为![]() ,
,
将![]() ,
,![]() 代入
代入![]() ,
,
得![]()
解得 ,
,
∴直线![]() 的解析式为
的解析式为![]()
设点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为
的坐标为![]()
![]()
设平行于![]() 的直线为
的直线为![]() ,
,
解方程组 ,
,
得![]()
由判别式![]() ,
,
得![]()
此时,直线![]() 与直线
与直线![]() 的距离即为
的距离即为![]() 的最大值.
的最大值.
求得,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
 中,
中, 是边
是边 上的一动点(不与点
上的一动点(不与点 、
、 重合),连接
重合),连接 ,点
,点 关于直线
关于直线 的对称点为
的对称点为 ,连接
,连接 并延长交
并延长交 于点
于点 ,连接
,连接 ,过点
,过点 作
作 交
交 的延长线于点
的延长线于点 ,连接
,连接 .
.(1)求证:
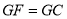 ;
;(2)用等式表示线段
 与
与 的数量关系,并证明.
的数量关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,为测量河岸两灯塔
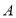 ,
,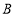 之间的距离,小明在河对岸
之间的距离,小明在河对岸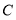 处测得灯塔
处测得灯塔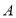 在北偏东
在北偏东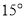 方向上,灯塔
方向上,灯塔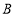 在东北方向上,小明沿河岸向东行走100米至
在东北方向上,小明沿河岸向东行走100米至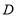 处,测得此时灯塔
处,测得此时灯塔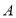 在北偏西
在北偏西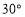 方向上,已知河两岸
方向上,已知河两岸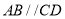 .
.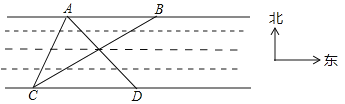
(1)求观测点
 到灯塔
到灯塔 的距离;
的距离;(2)求灯塔
 ,
,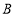 之间的距离.
之间的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】新华加工厂生产某种零件,该厂为了鼓励销售代理订货,提供了如下信息:
①每个零件的成本价为40元;②若一次订购该零件100个以内,出厂价为60元,若订购量超过100个时,每多订1个,订购的全部零件的出厂单价就降低0.02元;③实际出厂单价不能低于51元.根据以上信息,解答下列问题:
(1)当一次订购量达到 个时,零件的实际出厂单价降为51元;
(2)设一次订购量为
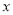 个,零件的实际出厂单价为
个,零件的实际出厂单价为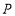 元,求
元,求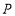 与
与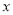 的函数表达式;
的函数表达式;(3)如果销售代理一次订购500个零件,该厂的利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了解旅游人数的变化情况,收集并整理了2017年1月至2019年12月期间的月接待旅游量(单位:万人次)的数据并绘制了统计图如下:
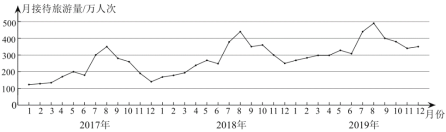
根据统计图提供的信息,下列推断不合理的是( )
A.2017年至2019年,各年的月接待旅游量高峰期大致在7,8月份
B.2019年的月接待旅游量的平均值超过300万人次
C.2017年至2019年,年接待旅游量逐年增加
D.2017年至2019年,各年下半年(7月至12月)的月接待旅游量相对于上半年(1月至6月)波动性更小,变化比较平稳
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x1,x2是关于x的方程x2+(3k+1)x+2k2+1=0的两个不相等实数根,且满足(x1﹣1)(x2﹣1)=8k2,则k的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正比例函数
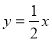 的图象与反比例函数
的图象与反比例函数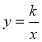 的图象交于
的图象交于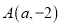 、
、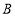 两点.
两点.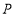 是第一象限内反比例函数图象上一点,过点
是第一象限内反比例函数图象上一点,过点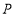 作
作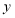 轴的平行线,交直线
轴的平行线,交直线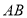 于点
于点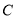 ,连接
,连接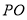 ,若
,若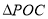 的面积为
的面积为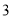 ,则点
,则点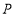 的坐标为_____________.
的坐标为_____________.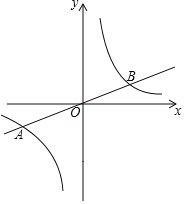
相关试题

