【题目】如图,在正方形![]() 中,
中,![]() 是边
是边![]() 上的一动点(不与点
上的一动点(不与点![]() 、
、![]() 重合),连接
重合),连接![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)用等式表示线段![]() 与
与![]() 的数量关系,并证明.
的数量关系,并证明.

参考答案:
【答案】(1)详见解析;(2)![]() ,理由详见解析
,理由详见解析
【解析】
1)如图1,连接DF,根据对称得:△ADE≌△FDE,再由HL证明Rt△DFG≌Rt△DCG,可得结论;
(2)如图2,作辅助线,构建AM=AE,先证明∠EDG=45°,得DE=EH,证明△DME≌△EBH,则EM=BH,根据等腰直角△AEM得:![]() ,得结论;
,得结论;
证明:(1)如图1,连接![]() ,
,
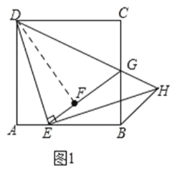
∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
∵点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
∵![]()
∴![]() ≌
≌![]() (
(![]() ),
),
∴![]() ;
;
(2)![]() ,理由是:
,理由是:
如图2,在线段![]() 上截取
上截取![]() ,使
,使![]() ,
,
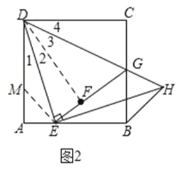
∵![]() ,
,
∴![]() ,
,
由(1)知:![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
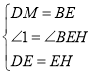
∴![]() ≌
≌![]()
∴![]() ,
,
![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①, 已知△ABC中, ∠BAC=90°, AB=AC, AE是过A的一条直线, 且B、C在AE的异侧, BD⊥AE于D, CE⊥AE于E.

(1)求证: BD=DE+CE.
(2)若直线AE绕A点旋转到图②位置时(BD<CE), 其余条件不变, 问BD与DE、CE的数量关系如何? 请给予证明;
(3)若直线AE绕A点旋转到图③位置时(BD>CE), 其余条件不变, 问BD与DE、CE的数量关系如何? 请直接写出结果, 不需证明.
(4)根据以上的讨论,请用简洁的语言表达BD与DE,CE的数量关系。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,∠B=55°,点D是斜边AB的中点,那么∠ACD的度数为( )
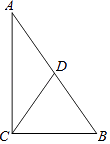
A.15°
B.25°
C.35°
D.45° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,在平面直角坐标系中,点A,B,E分别是x轴和y轴上的任意点. BD是∠ABE的平分线,BD的反向延长线与∠OAB的平分线交于点C.
探究: (1)求∠C的度数.
发现: (2)当点A,点B分别在x轴和y轴的正半轴上移动时,∠C的大小是否发生变化?若不变,请直接写出结论;若发生变化,请求出∠C的变化范围.
应用:(3)如图2在五边形ABCDE中,∠A+∠B+∠E=310°,CF平分∠DCB,CF的反向延长线与∠EDC外角的平分线相交于点P,求∠P的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道三角形任意两条中线的交点是三角形的重心.重心有如下性质:重心到顶点的距离是重心到对边中点距离的2倍,请利用该性质解决问题:
(1)如图1,在
 中,
中, 、
、 是中线,
是中线, 于点
于点 ,若
,若 ,
, ,则
,则 ,
, ;
;(2)如图1,在
 中,
中, ,
, ,
, ,
, 、
、 是中线,
是中线, 于点
于点 ,猜想
,猜想 、
、 、
、 三者之间的关系并证明;
三者之间的关系并证明;(3)如图2,在
 中,点
中,点 ,
, ,
, 分别是
分别是 ,
, ,
, 的中点,
的中点, ,
, ,
, .求AF的长.
.求AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某班同学在一次体检中每分钟心跳的频数分布直方图(次数均为整数).已知该班只有5位同学的心跳每分钟75次,请观察图示,指出下列说法不一定正确的是( )

A. 数据75落在第二小组 B. 第四小组的频率为0.1
C. 心跳为每分钟75次的人数占该班体检人数的
 D. 心跳是65次的人数最多
D. 心跳是65次的人数最多 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,点 D 是边 BC 上的点(与 B、C 两点不重合),过点 D作 DE∥AC,DF∥AB,分别交 AB、AC 于 E、F 两点,下列说法正确的是( )
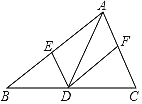
A. 若 AD 平分∠BAC,则四边形 AEDF 是菱形
B. 若 BD=CD,则四边形 AEDF 是菱形
C. 若 AD 垂直平分 BC,则四边形 AEDF 是矩形
D. 若 AD⊥BC,则四边形 AEDF 是矩形
相关试题

