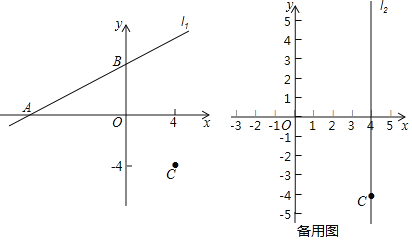
【题目】在平面直角坐标系xOy中,直线l1:y=![]() x+b与x轴交于点A,与y轴交于点B,且点C的坐标为(4,﹣4).
x+b与x轴交于点A,与y轴交于点B,且点C的坐标为(4,﹣4).
(1)点A的坐标为 ,点B的坐标为 ;(用含b的式子表示)
(2)当b=4时,如图所示.连接AC,BC,判断△ABC的形状,并证明你的结论;
(3)过点C作平行于y轴的直线l2,点P在直线l2上.当﹣5<b<4时,在直线l1平移的过程中,若存在点P使得△ABP是以AB为直角边的等腰直角三角形,请直接写出所有满足条件的点P的纵坐标.
参考答案:
【答案】(1)(﹣2b,0),(0,b);(2)△ABC是等腰直角三角形,理由见解析;(3)存在,满足条件的点P坐标为(4,﹣![]() )或(4,8)或(4,﹣12),理由见解析
)或(4,8)或(4,﹣12),理由见解析
【解析】
(1)由待定系数法即可解决问题;
(2)△ABC是等腰直角三角形.根据两点间距离公式以及勾股定理的逆定理即可判断;
(3)分三种情形①如图2中,当AB=AP,∠BAP=90°,设直线l2交x轴于N.设OB=m,则OA=2m,理由全等三角形的性质,构建方程解决问题.②如图3中,当AB=AP′,∠BAP′=90°时,设OB=m,OA=2m,理由全等三角形的性质构建方程解决问题.③如图3中,当AB=PB,∠ABP=90°时,同法可得.
解:(1)对于直线y=![]() x+b,令x=0,得到y=b,令y=0,得到x=﹣2b,
x+b,令x=0,得到y=b,令y=0,得到x=﹣2b,
∴A(﹣2b,0),B(0,b)
故答案为(﹣2b,0),(0,b);
(2)△ABC是等腰直角三角形.
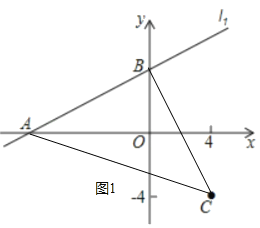
理由:∵b=4,
∴A(﹣8,0),B(0,4),∵C(4,﹣4),
∴AB=![]() ,
,
∴AB=BC,
∵AB2+BC2=(4![]() )2+(4
)2+(4![]() )2=160,AC2=160,
)2=160,AC2=160,
∴AB2+BC2=AC2,
∴∠ABC=90°,
∴△ABC是等腰直角三角形;
(3)①如图2中,当AB=AP,∠BAP=90°,设直线l2交x轴于N.
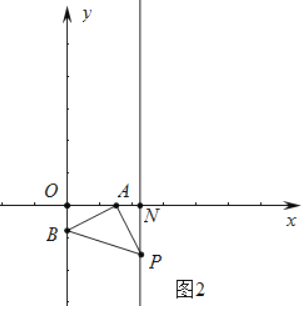
∵OA=2OB,设OB=m,则OA=2m,
由△AOB≌△PNA,可得AN=OB=m,PN=OA=2m,
∴ON=3m=4,
∴m=![]() ,
,
∴PM=![]() ,
,
∴P(4,﹣![]() ).
).
②如图3中,当AB=AP′,∠BAP′=90°时,设OB=m,OA=2m,
由△AOB≌△P′NA,可得AN=OB=m,P′N=OA=2m,
∵ON=4=2m﹣m,
∴m=4,
∴P′N=8,
∴P′(4,8),
③如图3中,当AB=PB,∠ABP=90°时,同法可得P(4,﹣12).
综上所述,满足条件的点P坐标为(4,﹣![]() )或(4,8)或(4,﹣12).
)或(4,8)或(4,﹣12).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016山东省菏泽市)如图,△ACB和△DCE均为等腰三角形,点A,D,E在同一直线上,连接BE.
(1)如图1,若∠CAB=∠CBA=∠CDE=∠CED=50°
①求证:AD=BE;
②求∠AEB的度数.
(2)如图2,若∠ACB=∠DCE=120°,CM为△DCE中DE边上的高,BN为△ABE中AE边上的高,试证明:AE=
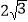 CM+
CM+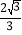 BN.
BN.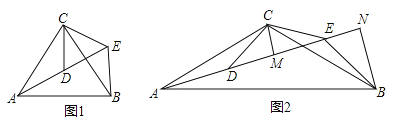
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC内接于
 ,AB是直径,OD∥AC,AD=OC.
,AB是直径,OD∥AC,AD=OC.(1)求证:四边形OCAD是平行四边形;
(2)填空:①当∠B= 时,四边形OCAD是菱形;
②当∠B= 时,AD与
 相切.
相切.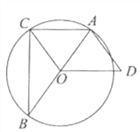
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数y=
 的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
的图象交于点A(﹣3,m+8),B(n,﹣6)两点.(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,一个正方体纸盒的棱长为6厘米,则它的表面积为 平方厘米.

(2)将该正方体的一些棱剪开展成一个平面图形,则需要剪卉 条棱,并求这个平面图形的周长.
(3)如图2,一个长方体纸盒的长、宽、高分别是a厘米、b厘米、c厘米(a>b>c)将它的一些棱剪开展成一个平面图形,求这个平面图形的最大周长,画出周长最大的平面图形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,求四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购. 经调查:购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.
(1)求甲、乙两种型号设备的价格;
(2)该公司经预算决定购买节省能源的新设备的资金不超过110万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备的产量为240吨/月,乙型设备的产量为180吨/月.若每月要求总产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
相关试题

