Question

【题目】已知，如图，四边形ABCD中，AB=3cm，AD=4cm，BC=13cm，CD=12cm，且∠A=90°，求四边形ABCD的面积.

Answer 1

【答案】84

【解析】首先连接BD，再利用勾股定理计算出BD的长，再根据勾股定理逆定理计算出∠D=90°，然后计算出直角三角形ABD和直角三角形BDC的面积，即可算出答案．

解：连接BD，

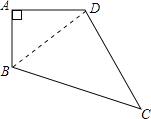
∵∠A=90°，AB=3cm，AD=4cm，
∴BD===5（cm），
∵52+122=132，
∴BD2+CD2=CB2，
∴∠BDC=90°，
∴S△DBC=×DB×CD=×5×12=30（cm2），
S△ABD=×3×4=6（cm2），
∴四边形ABCD的面积为30+6=36（cm2），
故答案为：36（cm2）．

“点睛”此题主要考查了勾股定理，以及勾股定理的逆定理，解决此题的关键是算出BD的长，△BDC是直角三角形．