【题目】如图,已知![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,D是AB边的中点,E是AC边上一点,联结DE,过点D作
,D是AB边的中点,E是AC边上一点,联结DE,过点D作![]() 交BC边于点F,联结EF.
交BC边于点F,联结EF.
(1)如图1,当![]() 时,求EF的长;
时,求EF的长;
(2)如图2,当点E在AC边上移动时, ![]() 的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出
的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出![]() 的正切值;
的正切值;
(3)如图3,联结CD交EF于点Q,当![]() 是等腰三角形时,请直接写出BF的长.
是等腰三角形时,请直接写出BF的长.

参考答案:
【答案】(1)![]() ;(2)不变;(3)
;(2)不变;(3)![]() 或3或
或3或![]() .
.
【解析】试题分析:(1)由已知条件易求DE=3,DF=4,再由勾股定理EF=5;
(2)过点![]() 作
作![]() ,
, ![]() ,垂足分别为点
,垂足分别为点![]() 、
、![]() ,由(1)可得DH=3,DG=4;再证
,由(1)可得DH=3,DG=4;再证![]() ,即可得出结论;
,即可得出结论;
(3)分三种情况讨论即可.
(1)∵![]() ,
, ![]()
∴![]()
∵![]()
∴![]()
∵![]() 是
是![]() 边的中点
边的中点
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
∵在![]() 中,
中, ![]()
∴![]()
∵![]()
∴![]()
又∵![]()
∴四边形![]() 是矩形
是矩形
∴![]()
∵在![]() 中,
中, ![]()
∴![]()
(2)不变
过点![]() 作
作![]() ,
, ![]() ,垂足分别为点
,垂足分别为点![]() 、
、![]()
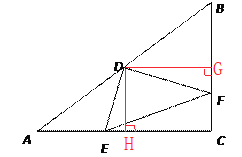
由(1)可得![]() ,
, ![]()
∵![]() ,
, ![]()
∴![]()
又∵![]() ,
,
∴四边形![]() 是矩形
是矩形
∴![]()
∵![]()
∴![]() 即
即![]()
又∵![]()
∴![]()
∴![]()
∵![]()
∴![]()
(3)1° 当![]() 时,易证
时,易证![]() ,即
,即![]()
又∵![]() ,D是AB的中点
,D是AB的中点
∴![]()
∴![]()
2° 当![]() 时,易证
时,易证![]()
∵在![]() 中,
中, ![]()
∴设![]() ,则
,则![]() ,
, ![]()
当![]() 时,易证
时,易证![]() ,
,
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∵![]()
∴
∴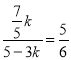 解得
解得![]()
∴![]()
∴![]()
3° 在BC边上截取BK=BD=5,由勾股定理得出![]()
当![]() 时,易证
时,易证![]()
∴设![]() ,则
,则![]() ,
, ![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴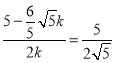 解得
解得![]()
∴![]()
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解学生对“A:古诗词,B:国画,C:京剧,D:书法”等中国传统文化项目的最喜爱情况,在全校范围内随机抽取部分学生进行问卷调查(每人限选一项),并将调查结果绘制成如下不完整的统计图.
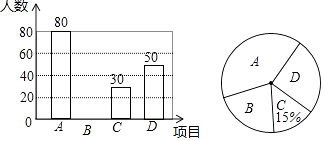
请结合统计图回答下列问题:
(1)在这次调查中,一共调查了名学生;在扇形统计图中,项目B对应扇形的圆心角是度;
(2)如果该校共有2000名学生,请估计该校最喜爱项目A的学生有多少人?
(3)若该校在A、B、C、D四项中任选两项成立课外兴趣小组,请用画树状图(或列表)计算恰好选中项目A和D的概率.
故答案为:200,72; -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司计划从本地向甲、乙两地运送海产品进行销售.本地与甲、乙两地都有铁路和公路相连(如图所示),铁路的单位运价为2元/(吨千米),公路的单位运价为3元/(吨千米)
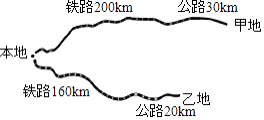
(1)若公司计划往甲、乙两地运输海产品共需铁路运费3680元,公路运费780元,求计划从本地向甲乙两地运输海产品各多少吨?
(2)经市场调查发现,甲地海产品的实际需求量比计划减少a(a>0)吨,但运到甲、乙两地的总量不变,且运到甲地的海产品不少于运到乙地的海产品,当a为多少时,实际总运费w最低?最低总运费是多少? (参考公式:货运运费=单位运价×运输里程×货物重量) -
科目: 来源: 题型:
查看答案和解析>>【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质量的差值(单位:千克)
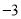
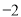

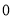
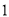
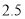
筐 数
1
4
2
3
2
8
(1)20筐白菜中,最重的一筐比最轻的一筐重______千克;
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价
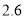 元,则出售这20筐白菜可卖多少元?
元,则出售这20筐白菜可卖多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填在相应的大括号里:
-3,0.2,0,-|+
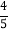 |,-5%,-
|,-5%,-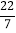 ,|-9|,-(-1),-23,+3
,|-9|,-(-1),-23,+3 .
.(1)正整数集合:{ …};
(2)负分数集合:{ …};
(3)负数集合:{ …};
(4)整数集合:{ …};
(5)分数集合:{ …};
(6)非负数集合:{ …}.
-
科目: 来源: 题型:
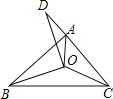
查看答案和解析>>【题目】如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,AD=AO,若∠BAC=80°,则∠BCA的度数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l与⊙O相离,过点O作OA⊥l,垂足为A,OA交⊙O于点B,点C在直线l上,连接CB并延长交⊙O于点D,在直线l上另取一点P,使∠PCD=∠PDC.
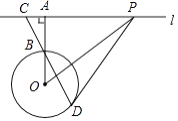
(1)求证:PD是⊙O的切线;
(2)若AC=1,AB=2,PD=6,求⊙O的半径r和△PCD的面积.
相关试题

