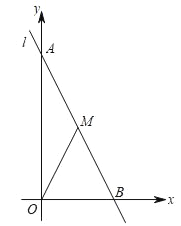
【题目】如图,已知在平面直角坐标中,直线l:y=﹣2x+6分别交两坐标于A、B两点,M是级段AB上一个动点,设点M的横坐标为x,△OMB的面积为S.
(1)写出S与x的函数关系式;
(2)当△OMB的面积是△OAB面积的![]() 时,求点M的坐标;
时,求点M的坐标;
(3)当△OMB是以OB为底的等腰三角形,求它的面积.
参考答案:
【答案】(1)S=﹣3x+9(0≤x<3);(2)M(1,4);(3)![]() .
.
【解析】
(1)根据x轴的坐标特点求出点B坐标,再表示出点M坐标,最后利用三角形的面积公式即可得出结论;
(2)根据y轴的坐标特点求出点A坐标,进而利用三角形的面积公式求出△AOB的面积,进而求出△OBM的面积,即可得出结论;
(3)先判定点M是OB的垂直平分线上,进而求出M的坐标,即可得出结论.
(1)针对于直线l:y=﹣2x+6,
令y=0,则﹣2x+6=0,
∴x=3,
∴B(3,0),
∴OB=3,
∵点M在线段AB上,
∴M(x,﹣2x+6),
∴S=S△OBM=![]() ×3×(﹣2x+6)=﹣3x+9(0≤x<3),
×3×(﹣2x+6)=﹣3x+9(0≤x<3),
(2)针对于直线l:y=﹣2x+6,
令x=0,则y=6,
∴A(0,6),
∴S△AOB=![]() OAOB=
OAOB=![]() ×6×3=9,
×6×3=9,
∵△OMB的面积是△OAB面积的![]() ,
,
∴S△OBM=![]() ×9=6,
×9=6,
由(1)知,S△OBM=﹣3x+9(0≤<3),
∴﹣3x+9=6,
∴x=1,
∴M(1,4);
(3)∵△OMB是以OB为底的等腰三角形,
∴点M是OB的垂直平分线上,
∴点M(![]() ,3),
,3),
∴S△OBM=![]() ×3×3=
×3×3=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是坐标原点,菱形OABC的顶点A的坐标为(﹣3,4),顶点C在x轴的负半轴上,函数y=
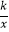 (x<0)的图象经过顶点B,则k的值为( )
(x<0)的图象经过顶点B,则k的值为( ) 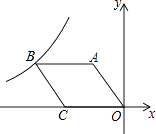
A.﹣12
B.﹣27
C.﹣32
D.﹣36 -
科目: 来源: 题型:
查看答案和解析>>【题目】定义一种对正整数n的“F运算”:①当n为奇数时,结果为3n+5;②当n为偶数时,结果为
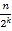 (其中k是使
(其中k是使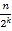 为奇数的正整数);并且运算重复进行.例如,取n=26,第3次“F运算”的结果是11.则:若n=449,则第449次“F运算”的结果是____.
为奇数的正整数);并且运算重复进行.例如,取n=26,第3次“F运算”的结果是11.则:若n=449,则第449次“F运算”的结果是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AD=5,点E、F是正方形ABCD内的两点,且AE=FC=3,BE=DF=4,则EF的长为( )

A.
B.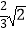
C.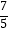
D.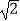
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,D为BC边上一个动点(D与B、C均不重合),AD=AE,∠DAE=60°,连接CE.
(1)求证:△ABD≌△ACE;
(2)求证:CE平分∠ACF;
(3)若AB=2,当四边形ADCE的周长取最小值时,求BD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则点B3的坐标是_____;点B2018的坐标是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】农夫将苹果树种在正方形的果园内.为了保护苹果树不怕风吹,他在苹果树的周围种针叶树.在下图里,你可以看到农夫所种植苹果树的列数(n)和苹果树数量及针叶树数量的规律:当n为某一个数值时,苹果树数量会等于针叶树数量,则n为( )

A.6
B.8
C.12
D.16
相关试题

