【题目】如图,在Rt△ABC中,∠C=90°,∠ABC的平分线交AC于点D,点O是AB上一点,⊙O过B、D两点,且分别交AB,BC于点E,F.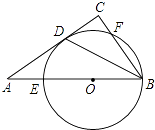
(1)求证:AC是⊙O的切线;
(2)已知AB=5,AC=4,求⊙O的半径r.
参考答案:
【答案】
(1)证明:连接OD,如图,
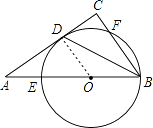
∵OB=OD,
∴∠ODB=∠OBD,
∵∠ABC的平分线交AC于点D,
∴∠OBD=∠DBC,
∴∠ODB=∠DBC,
∴OD∥BC,
∵∠C=90°,
∴∠ADO=90°,
∴OD⊥AC,
∴AC是⊙O的切线
(2)解:在Rt△ABC中,∵∠C=90°,AB=5,AC=4,
∴BC= ![]() =3,
=3,
∵OD∥BC,
∴△AOD∽△ABC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得r= ![]() .
.
【解析】要证AC是⊙O的切线,可知点D在圆上,因此连半径OD,再证明OD⊥AC即可,只需证出OD∥BC,再根据已知∠C=90°,即可得结论。
(2)在Rt△ABC中,利用勾股定理即可求出BC的长,再证明△AOD∽△ABC,运用相似三角形的性质,得对应边成比例,建立关于r的方程,求解即可。
【考点精析】本题主要考查了勾股定理的概念和切线的判定定理的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小明设计的“过直线外一点作这条直线的平行线”的尺规作图过程.
已知:如图
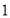 ,直线
,直线 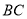 及直线
及直线 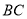 外一点
外一点 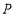 .
.求作:直线
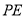 ,使得
,使得 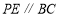 .
.作法:如图
 .
.①在直线
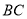 上取一点
上取一点  ,连接
,连接  ;
;②作
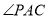 的平分线
的平分线 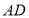 ;
;③以点
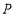 为圆心,
为圆心, 长为半径画弧,交射线
长为半径画弧,交射线 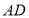 于点
于点 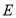 ;
;④作直线
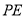 .
.所以直线
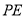 就是所求作的直线.根据小明设计的尺规作图过程.
就是所求作的直线.根据小明设计的尺规作图过程.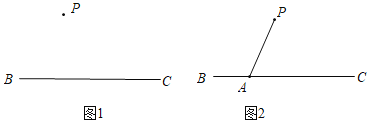
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:
 平分
平分 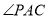 ,
,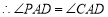 .
.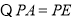 ,
,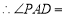
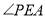 ,
,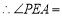 ,
,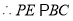 (____________________)(填推理依据).
(____________________)(填推理依据). -
科目: 来源: 题型:
查看答案和解析>>【题目】请在横线上和括号内填上推导内容或依据.
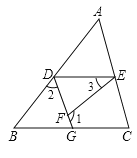
如图,已知
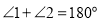 ,
, 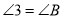 ,求证:
,求证: 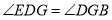 .
.
证明:
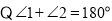 (已知),
(已知),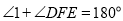 ( ),
( ),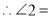 ( ).
( ).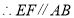 ( ).
( ).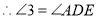 ( ).
( ).∵
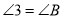 (已知),
(已知),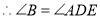 ( ).
( ).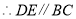 ( ).
( ).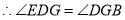 ( ).
( ). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,直线
 ,
,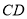 相交于点
相交于点  ,
, .
.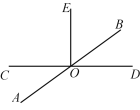
(1)若
 ,求
,求  的度数;
的度数;(2)若
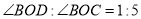 ,求
,求 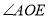 的度数;
的度数;(3)在(
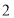 )的条件下,过点
)的条件下,过点  作
作  ,请直接写出
,请直接写出 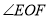 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某日在我国某岛附近海域有两艘自西向东航行的海监船A、B,船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留小数点后一位)
参考数据: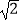 ≈1.414,
≈1.414, 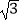 ≈1.732,
≈1.732, 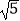 ≈2.236.
≈2.236.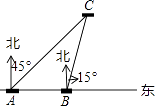
-
科目: 来源: 题型:
查看答案和解析>>【题目】小云想用7天的时间背诵若干首诗词,背诵计划如下:
①将诗词分成4组,第i组有
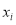 首,i =1,2,3,4;
首,i =1,2,3,4;②对于第i组诗词,第i天背诵第一遍,第(
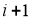 )天背诵第二遍,第(
)天背诵第二遍,第(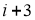 )天背诵第三遍,三遍后完成背诵,其它天无需背诵,
)天背诵第三遍,三遍后完成背诵,其它天无需背诵,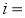 1,2,3,4;
1,2,3,4;第1天
第2天
第3天
第4天
第5天
第6天
第7天
第1组
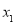
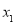
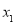
第2组
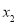
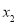
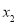
第3组
第4组
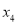
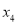
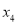
③每天最多背诵14首,最少背诵4首.
解答下列问题:
(1)填入
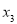 补全上表;
补全上表;(2)若
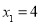 ,
, ,
, ,则
,则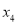 的所有可能取值为______;
的所有可能取值为______;(3)7天后,小云背诵的诗词最多为______首.
-
科目: 来源: 题型:
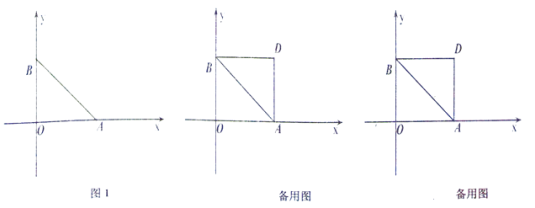
查看答案和解析>>【题目】如图1,在平面直角坐标系中,点O为坐标原点,点A(a,0)、B(b,O)分别在x轴正半轴和y轴正半轴上,且
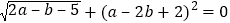 ,点P从原点出发以每秒2个单位长度的速度沿x轴正半轴方向运动.
,点P从原点出发以每秒2个单位长度的速度沿x轴正半轴方向运动.(1)求点A、B的坐标;
(2)连接PB,设三角形ABP的面积为s,点P的运动时间为t,请用含t的式子表示s,并直接写出t的取值范围;
(3)在(2)的条件下,将线段OB沿x轴正方向平移,使点O与点A重合,点B的对应点为点D,连接BD,将线段PB沿x轴正方向平移,使点B与点D重合,点P的对应点为点Q,取DQ的中点H,是否存在t的值,使三角形ABP的面积等于三角形ADH的面积?若存在,求出t的值;若不存在,请说明理由.
相关试题

