【题目】请在横线上和括号内填上推导内容或依据.
如图,已知 ![]() ,
, ![]() ,求证:
,求证: ![]() .
.
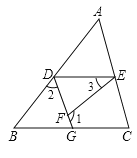
证明: ![]() (已知),
(已知),
![]() ( ),
( ),
![]() ( ).
( ).
![]() ( ).
( ).
![]() ( ).
( ).
∵![]() (已知),
(已知),
![]() ( ).
( ).
![]() ( ).
( ).
![]() ( ).
( ).
参考答案:
【答案】邻补角定义;∠DFE;同角的补角相等;内错角相等,两直线平行;两直线平行,内错角相等;等量代换;同位角相等,两直线平行;两直线平行,内错角相等.
【解析】
首先利用“同角的补角相等”可得![]() ∠DFE,由此根据“内错角相等,两直线平行”得出EF∥AB,接着根据“两直线平行,内错角相等”得出
∠DFE,由此根据“内错角相等,两直线平行”得出EF∥AB,接着根据“两直线平行,内错角相等”得出![]() ,据此结合
,据此结合![]() 即可通过等量代换得知
即可通过等量代换得知![]() ,最后再次利用平行线的性质及判定进一步证明即可.
,最后再次利用平行线的性质及判定进一步证明即可.
∵![]() 180°(已知),
180°(已知),
![]() 180°(邻补角定义),
180°(邻补角定义),
∴![]() ∠DFE(同角的补角相等),
∠DFE(同角的补角相等),
∴EF∥AB(内错角相等,两直线平行),
∴![]() (两直线平行,内错角相等),
(两直线平行,内错角相等),
∵![]() (已知),
(已知),
∴![]() (等量代换),
(等量代换),
∴DE∥BC(同位角相等,两直线平行),
∴![]() (两直线平行,内错角相等).
(两直线平行,内错角相等).
故答案为:邻补角定义;∠DFE;同角的补角相等;内错角相等,两直线平行;两直线平行,内错角相等;等量代换;同位角相等,两直线平行;两直线平行,内错角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A在第一象限,点B(a,0),点C(0,b)分别在x轴,y轴上,其中a,b是二元一次方程
 的解,且a为不等式
的解,且a为不等式 的最大整数解.
的最大整数解.(1)证明:OB=OC;
(2)如图1,连接AB,过点A作AD⊥AB交y轴于点D,在射线AD上截取AE=AB,连接CE,取CE的中点F,连接AF并延长至点G,使FG=AF,连接CG,OA.当点A在第一象限内运动(AD不经过点C)时,证明:∠OAF的大小不变;

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子中,共有“一白三黑”四个围棋子,其除颜色外无其他区别.
(1)随机地从盒子中取出1子,则提出的是白子的概率是多少?
(2)随机地从盒子中取出1子,不放回再取出第二子,请用画树状或列表的方式表示出所有可能的结果,并求出恰好取出“一黑一白”的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小明设计的“过直线外一点作这条直线的平行线”的尺规作图过程.
已知:如图
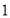 ,直线
,直线 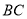 及直线
及直线 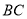 外一点
外一点 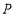 .
.求作:直线
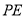 ,使得
,使得 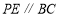 .
.作法:如图
 .
.①在直线
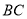 上取一点
上取一点  ,连接
,连接  ;
;②作
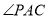 的平分线
的平分线 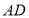 ;
;③以点
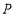 为圆心,
为圆心, 长为半径画弧,交射线
长为半径画弧,交射线 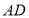 于点
于点 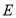 ;
;④作直线
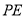 .
.所以直线
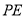 就是所求作的直线.根据小明设计的尺规作图过程.
就是所求作的直线.根据小明设计的尺规作图过程.
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:
 平分
平分  ,
,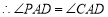 .
.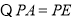 ,
,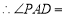
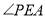 ,
,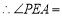 ,
,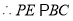 (____________________)(填推理依据).
(____________________)(填推理依据). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,直线
 ,
,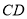 相交于点
相交于点  ,
, .
.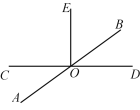
(1)若
 ,求
,求  的度数;
的度数;(2)若
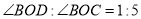 ,求
,求 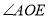 的度数;
的度数;(3)在(
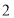 )的条件下,过点
)的条件下,过点  作
作  ,请直接写出
,请直接写出 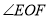 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠ABC的平分线交AC于点D,点O是AB上一点,⊙O过B、D两点,且分别交AB,BC于点E,F.
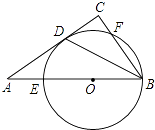
(1)求证:AC是⊙O的切线;
(2)已知AB=5,AC=4,求⊙O的半径r. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某日在我国某岛附近海域有两艘自西向东航行的海监船A、B,船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留小数点后一位)
参考数据: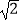 ≈1.414,
≈1.414, 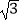 ≈1.732,
≈1.732, 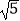 ≈2.236.
≈2.236.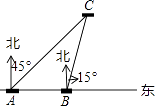
相关试题

