【题目】如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )
A.
B.
C.
D.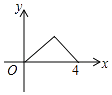
参考答案:
【答案】B
【解析】解:过A点作AH⊥BC于H,
∵△ABC是等腰直角三角形,
∴∠B=∠C=45°,BH=CH=AH= ![]() BC=2,
BC=2,
当0≤x≤2时,如图1,
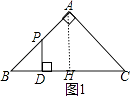
∵∠B=45°,
∴PD=BD=x,
∴y= ![]() xx=
xx= ![]() x2;
x2;
当2<x≤4时,如图2,
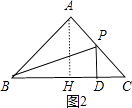
∵∠C=45°,
∴PD=CD=4﹣x,
∴y= ![]() (4﹣x)x=﹣
(4﹣x)x=﹣ ![]() x2+2x,
x2+2x,
故选B
【考点精析】本题主要考查了函数的图象的相关知识点,需要掌握函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在平面直角坐标系中,已知点A(-5,0),B(5,0),D(2,7).
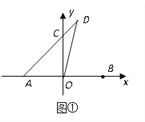
(1)若点C为AD与y轴的交点,求C点的坐标;【提示:设C点的坐标为(0,x)】
(2)动点P从B点出发以每秒1个单位的速度沿BA方向运动,同时动点Q从C点出发,也以每秒1个单位的速度沿y轴正半轴方向运动.(当P点运动到A点时,两点都停止运动,如图②所示).设从出发起运动了x秒.
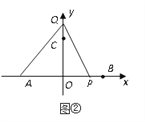
①请用含x的代数式分别表示P、Q两点的坐标;
②当x=2时,y轴上是否存在一点E,使得△AQE的面积与△APQ的面积相等?若存在,求E点的坐标,若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如右图,在
 中,
中, ,
, ,垂足为点
,垂足为点 ,有下列说法:①点
,有下列说法:①点 与点
与点 的距离是线段
的距离是线段 的长;②点
的长;②点 到直线
到直线 的距离是线段
的距离是线段 的长;③线段
的长;③线段 是
是 边
边 上的高;④线段
上的高;④线段 是
是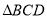 边
边 上的高.
上的高.上述说法中,正确的个数为( )

A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
 ,P为x轴正半轴一动点,BC平分
,P为x轴正半轴一动点,BC平分 ,PC平分
,PC平分 ,OD平分
,OD平分
 求
求 的度数;
的度数; 求证:
求证: ;
; 在运动中,
在运动中, 的值是否变化?若发生变化,说明理由;若不变,求其值.
的值是否变化?若发生变化,说明理由;若不变,求其值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
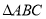 中,点
中,点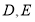 分别在边
分别在边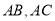 上,
上,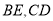 相交于点
相交于点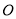 ,如果已知
,如果已知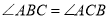 ,那么还不能判定
,那么还不能判定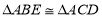 ,补充下列一个条件后,仍无法判定
,补充下列一个条件后,仍无法判定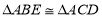 的是( )
的是( )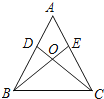
A.
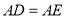 B.
B.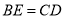
C.
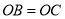 D.
D.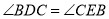
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A
B
载客量(人/辆)
45
30
租金(元/辆)
400
280
红星中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆)
载客量(人)
租金(元)
A
x
45x
400x
B
5-x
(2)若要保证租车费用不超过1900元,求x的最大值;
(3)在(2)的条件下,若七年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列4个命题:①两边及其中一边上的中线对应相等的两个三角形全等;②两边及其中一边上的高对应相等的两个三角形全等;③两边及一角对应相等的两个三角形全等;④有两角及其中一角的角平分线对应相等的两个三角形全等.其中正确的的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

