【题目】定义新运算:对于任意实数a,b,都有a![]() b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算,比如:2
b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算,比如:2![]() 5=2×(2-5)+1=2×(-3)+1=-6+1=-5.
5=2×(2-5)+1=2×(-3)+1=-6+1=-5.
(1)求(-2) ![]() 3的值;
3的值;
(2)若3![]() x的值小于13,求x的取值范围,并在如图所示的数轴上表示出来.
x的值小于13,求x的取值范围,并在如图所示的数轴上表示出来.
![]()
参考答案:
【答案】(1)11;(2)x>-1.
【解析】试题分析:(1)按照定义新运算a⊕b=a(a-b)+1,求解即可;
(2)先按照定义新运算a⊕b=a(a-b)+1,得出3⊕x,再令其小于13,得到一元一次不等式,解不等式求出x的取值范围,即可在数轴上表示.
试题解析:(1)∵a⊕b=a(a-b)+1,
∴(-2)⊕3=-2×(-2-3)+1=10+1=11; (2)∵3⊕x<13,
∴3(3-x)+1<13,
∴9-3x+1<13,
∴-3x<3,
∴x>-1.
在数轴上表示如下.
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
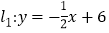 分别与
分别与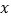 轴、
轴、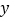 轴交于点
轴交于点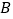 、
、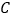 ,且与直线
,且与直线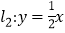 交于点
交于点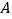 .
.
(1)若
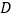 是线段
是线段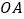 上的点,且
上的点,且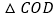 的面积为
的面积为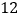 ,求直线
,求直线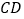 的函数表达式.
的函数表达式.(
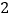 )在(
)在(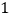 )的条件下,设
)的条件下,设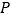 是射线
是射线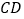 上的点,在平面内是否存在点
上的点,在平面内是否存在点 ,使以
,使以 、
、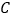 、
、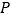 、
、 为顶点的四边形是菱形?若存在,直接写出点
为顶点的四边形是菱形?若存在,直接写出点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD的顶点B,D都在反比例函数y=
 (x>0)的图象上,点D的坐标为(2,6),AB平行于x轴,点A的坐标为(0,3),将这个平行四边形像左平移2个单位,再向下平移3个单位后,点C的坐标为( )
(x>0)的图象上,点D的坐标为(2,6),AB平行于x轴,点A的坐标为(0,3),将这个平行四边形像左平移2个单位,再向下平移3个单位后,点C的坐标为( )
A.(4,3) B.(2,3) C.(1,4) D.(2,4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某篮球运动员去年共参加40场比赛,其中3分球的命中率为0.25,平均每场有12次3分球未投中.
(1)该运动员去年的比赛中共投出多少个3分球?共投中多少个3分球?
(2)在其中的一场比赛中,该运动员3分球共出手20次,小亮说,该运动员这场比赛中一定投中了5个3分球,你认为小亮的说法正确吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,动点P在函数y=
 (x>0)的图象上运动,PM⊥x轴于M,PN⊥y轴于N,线段PM、PN分别与直线AB:y=-x+1交于点E、F,且AFBE的值为1,则k为________.
(x>0)的图象上运动,PM⊥x轴于M,PN⊥y轴于N,线段PM、PN分别与直线AB:y=-x+1交于点E、F,且AFBE的值为1,则k为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
 -
- +(-2)-3;
+(-2)-3;(2)(-3ab)·(-a2c)3·5b2(c2)3;
(3)x2(x-1)-x(x2+x-1);
(4)(a+3)(a-1)+a(a-2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在某住房小区的建设中,为了提高业主的宜居环境,小区准备在一个长为(4a+3b)米,宽为(2a+3b)米的长方形草坪上修建两条宽为b米的通道.
(1)通道的面积是多少平方米?
(2)剩余草坪的面积是多少平方米?

相关试题

