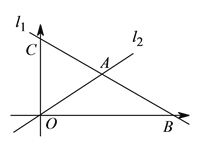
【题目】如图,在平面直角坐标系中,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() ,且与直线
,且与直线![]() 交于点
交于点![]() .
.

(1)若![]() 是线段
是线段![]() 上的点,且
上的点,且![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的函数表达式.
的函数表达式.
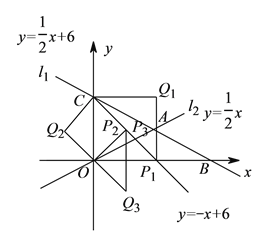
(![]() )在(
)在(![]() )的条件下,设
)的条件下,设![]() 是射线
是射线![]() 上的点,在平面内是否存在点
上的点,在平面内是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,直接写出点
为顶点的四边形是菱形?若存在,直接写出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
参考答案:
【答案】(1)![]() (2)存在,
(2)存在,![]() 或
或![]() 或
或![]()
【解析】试题分析:(1)对于直线![]() 解析式,令x=0,求出y的值,确定C的坐标;根据D在直线OA上,设
解析式,令x=0,求出y的值,确定C的坐标;根据D在直线OA上,设![]() ,表示出△COD面积,把已知面积代入求出x的值,确定出D坐标,利用待定系数法求出CD解析式即可;
,表示出△COD面积,把已知面积代入求出x的值,确定出D坐标,利用待定系数法求出CD解析式即可;
(2)在(1)的条件下,设P是射线CD上的点,在平面内存在点Q,使以O、C、P、Q为顶点的四边形是菱形,如图所示,分三种情况考虑:①当四边形![]() 为菱形时,由
为菱形时,由![]() ,得到四边形
,得到四边形![]() 为正方形;②当四边形
为正方形;②当四边形![]() 为菱形时;③当四边形
为菱形时;③当四边形![]() 为菱形时;分别求出Q坐标即可.
为菱形时;分别求出Q坐标即可.
解:(![]() )设
)设![]() .
.
∵![]() 且
且![]() ,
,
∴![]()
∴![]()
∴![]() .
.
令![]() 直线解析式为
直线解析式为![]()
把![]() ,
,![]() 代入得:
代入得:
![]()
∴![]() .
.
∴![]() .
.
(![]() )存在.
)存在.
①当四边形![]() 为菱形时.
为菱形时.
∵![]() 得四边形
得四边形![]() 为正方形
为正方形
∴![]() ,
,
即![]() .
.
②当四边形![]() 为菱形时
为菱形时
∵![]() 得
得![]()
![]() 代入
代入![]() 得
得![]() ,
,
∴![]() .
.
③当四边形![]() 为菱形时
为菱形时
∴![]()
∴![]()
综上得点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】附加题:
(1).填空:请用文字语言叙述勾股定理的逆定理:__________.
勾股定理的逆定理所给出的判定一个三角形是直角三角形的方法,和学过的一些其它几何图形的判定方法不同,它通过计算来判断.实际上计算在几何中也是很重要的,从数学方法这个意义上讲,我们学习勾股定理的逆定理,更重要的是拓展思维,进一步体会数学中的各种方法.
(2).阅读:小明在学习勾股定理后,尝试着利用计算的方法进行论证,解决了如下问题:
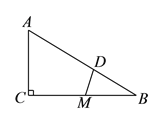
如图
 中,
中,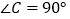 ,
, 是
是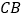 的中点,
的中点,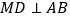 于
于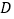 ,请说明三条线段
,请说明三条线段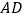 、
、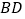 、
、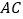 总能构成一个直角三角形.
总能构成一个直角三角形.证明:设
 ,
,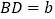 ,
,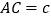 ,
,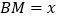 ,
,∵
 是
是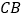 的中点,∴
的中点,∴ ,
,在
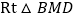 中,
中, ,
,在
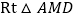 中,
中,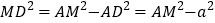 ,
,消去
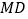 ,得
,得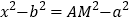 ,从而,
,从而,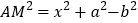 ,
,又因为在
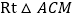 中,
中,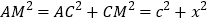 ,
,消去
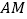 得
得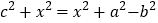 ,消去
,消去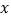 ,所以
,所以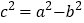 ,即
,即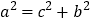 .
.所以,三条线段
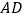 、
、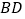 、
、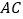 总能构成一个直角三角形.
总能构成一个直角三角形.可见,计算在几何证明中也是很重要的.小明正是利用代数中计算、消元等手段,结合相关定理来论证了几何问题.
(3).解决问题:在矩形
 中,点
中,点 、
、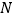 、
、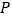 、
、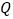 分别在边
分别在边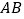 、
、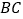 、
、 、
、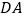 上,使得
上,使得 ,求证:四边形
,求证:四边形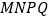 是平行四边形.
是平行四边形.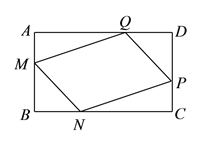
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C,D.

(1)∠ECD和∠EDC相等吗?说明理由.
(2)OC和OD相等吗?说明理由.
(3)OE是线段CD的垂直平分线吗?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某自行车厂计划一周生产自行车1400辆,平均每天生产200辆,但由于种种原因,实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产记为正、减产记为负):
星期
一
二
三
四
五
六
日
增减
+5
﹣2
﹣4
+12
﹣10
+16
﹣9
(1)根据记录的数据可知该厂星期六生产自行车______辆;
(2)根据记录的数据可知该厂本周实际生产自行车_____辆;
(3)产量最多的一天比产量最少的一天多生产自行车_____辆;
(4)该厂实行每周计件工资制,每生产一辆车可得50元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣20元,那么该厂工人这一周的工资总额是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD的顶点B,D都在反比例函数y=
 (x>0)的图象上,点D的坐标为(2,6),AB平行于x轴,点A的坐标为(0,3),将这个平行四边形像左平移2个单位,再向下平移3个单位后,点C的坐标为( )
(x>0)的图象上,点D的坐标为(2,6),AB平行于x轴,点A的坐标为(0,3),将这个平行四边形像左平移2个单位,再向下平移3个单位后,点C的坐标为( )
A.(4,3) B.(2,3) C.(1,4) D.(2,4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某篮球运动员去年共参加40场比赛,其中3分球的命中率为0.25,平均每场有12次3分球未投中.
(1)该运动员去年的比赛中共投出多少个3分球?共投中多少个3分球?
(2)在其中的一场比赛中,该运动员3分球共出手20次,小亮说,该运动员这场比赛中一定投中了5个3分球,你认为小亮的说法正确吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义新运算:对于任意实数a,b,都有a
 b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算,比如:2
b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算,比如:2 5=2×(2-5)+1=2×(-3)+1=-6+1=-5.
5=2×(2-5)+1=2×(-3)+1=-6+1=-5.(1)求(-2)
 3的值;
3的值;(2)若3
 x的值小于13,求x的取值范围,并在如图所示的数轴上表示出来.
x的值小于13,求x的取值范围,并在如图所示的数轴上表示出来.
相关试题

