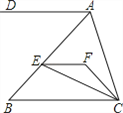
【题目】如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
参考答案:
【答案】20°.
【解析】试题分析:先由平行线的性质及∠DAC的度数算出∠ACB的度数,再根据∠ACF的度数求出∠FCB的度数,由CE平分∠BCF得出∠FCE=∠ECB,所以∠ECB的度数就求出来了,再由EF∥AD,AD∥BC,得出EF∥BC(平行公理推论),然后利用平行线性质推出∠FEC=∠ECB,从而得出∠FEC的度数.
试题解析:因为AD∥BC,∠DAC=120°,所以∠ACB=180°-120°=60°(两直线平行,同旁内角互补),又因为∠ACF=20°,所以∠BCF=60°-20°=40°,因为CE平分∠BCF,所以∠ECB=![]() ∠BCF=
∠BCF=![]() ×40°=20°,因为EF∥AD,AD∥BC,所以EF∥BC(根据平行公理推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行),所以∠FEC=∠ECB=20°(两直线平行,内错角相等).
×40°=20°,因为EF∥AD,AD∥BC,所以EF∥BC(根据平行公理推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行),所以∠FEC=∠ECB=20°(两直线平行,内错角相等).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若2x+1是﹣9的相反数,则x=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,半径OA⊥弦BC于点H,点D在优弧BC上
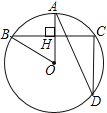
(1)若∠AOB=50°,求∠ADC的度数;
(2)若BC=8,AH=2,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数的图象与x轴、y轴分别相交于A、B两点,且与反比例函数y=
 (k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.
(k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.
(1)求一次函数解析式及反比例函数的解析式;
(2)若一次函数值大于反比例函数值,请求出相应的自变量x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,函数y=﹣x+4的图象与坐标轴交于A、B两点,点M(2,m)是直线AB上一点,点N与点M关于y轴对称.

(1)填空:m= ;
(2)点P在平面上,若以A、M、N、P为顶点的四边形是平行四边形,直接写出点P的坐标;
(3)如图2,反比例函数
 的图象经过N、E(x1,y1)、F(x2,y2)三点.且x1>x2,点E、F关于原点对称,若点E到直线MN的距离是点F到直线MN的距离的3倍,求E、F两点的坐标.
的图象经过N、E(x1,y1)、F(x2,y2)三点.且x1>x2,点E、F关于原点对称,若点E到直线MN的距离是点F到直线MN的距离的3倍,求E、F两点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一辆汽车离出发地的距离S(千米)和行驶时间t(小时)之间的函数图象.
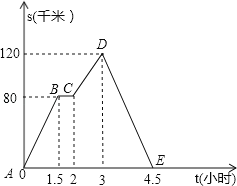
(1)汽车在DE段行驶了 小时;
(2)汽车在BC段停留了 小时;
(3)汽车出发1小时时,离出发地多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下表中,反比例函数的自变量x与函数y的对应值,可得p的值为( )
x
﹣2
1
y
3
p
A.3
B.1
C.﹣2
D.﹣6
相关试题

