Question

【题目】如图是一辆汽车离出发地的距离S（千米）和行驶时间t（小时）之间的函数图象．

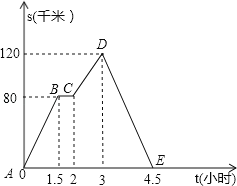
（1）汽车在DE段行驶了 小时；

（2）汽车在BC段停留了 小时；

（3）汽车出发1小时时，离出发地多少千米？

Answer 1

【答案】（1）1.5；

（2）0.5；

（3）行驶1小时时，离出发地千米．

【解析】

试题分析：（1）由DE段图象对应时间t的值可知；

（2）由BC段图象对应时间t的值可知；

（3）待定系数求得AB段解析式，令t=1求得对应s的值．

解：（1）汽车在DE段行驶时间为：4.5﹣3=1.5（小时），

故答案为：1.5；

（2）汽车在BC段停留时间为：2﹣1.5=0.5（小时），

故答案为：0.5；

（3）由图象可设AB段图象的函数表达式为y=kx，

当x=1.5时，y=80；

解得：k=，

即y=x，（0≤x≤1.5），

当x=1时，y=，

答：行驶1小时时，离出发地千米．