【题目】如图,一次函数的图象与x轴、y轴分别相交于A、B两点,且与反比例函数y=![]() (k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.
(k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.

(1)求一次函数解析式及反比例函数的解析式;
(2)若一次函数值大于反比例函数值,请求出相应的自变量x的取值范围.
参考答案:
【答案】(1)y=![]() .(2)﹣4<x<0或x>2.
.(2)﹣4<x<0或x>2.
【解析】
试题分析:(1)根据条件可先求得A点坐标,再根据中点,可求得C点坐标,然后根据待定系数法即可求得一次函数解析式及反比例函数的解析式;
(2)根据交点坐标和函数的图象即可求得.
解:(1)∵OA=OB,点B的坐标为(0,2),
∴点A(﹣2,0),点A、B在一次函数y=kx+b(k≠0)的图象上,
∴![]() ,解得k=1,b=2,
,解得k=1,b=2,
∴一次函数的解析式为y=x+2.
∵B是线段AC的中点,
∴点C的坐标为(2,4),
又∵点C在反比例函数y=![]() (k≠0)的图象上,
(k≠0)的图象上,
∴k=8
∴反比例函数的解析式为y=![]() .
.
(2)一次函数值大于反比例函数值的自变量x的取值范围﹣4<x<0或x>2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣2﹣(﹣3)=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若2x+1是﹣9的相反数,则x=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,半径OA⊥弦BC于点H,点D在优弧BC上
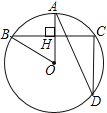
(1)若∠AOB=50°,求∠ADC的度数;
(2)若BC=8,AH=2,求⊙O的半径.
-
科目: 来源: 题型:
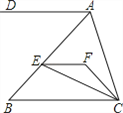
查看答案和解析>>【题目】如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,函数y=﹣x+4的图象与坐标轴交于A、B两点,点M(2,m)是直线AB上一点,点N与点M关于y轴对称.

(1)填空:m= ;
(2)点P在平面上,若以A、M、N、P为顶点的四边形是平行四边形,直接写出点P的坐标;
(3)如图2,反比例函数
 的图象经过N、E(x1,y1)、F(x2,y2)三点.且x1>x2,点E、F关于原点对称,若点E到直线MN的距离是点F到直线MN的距离的3倍,求E、F两点的坐标.
的图象经过N、E(x1,y1)、F(x2,y2)三点.且x1>x2,点E、F关于原点对称,若点E到直线MN的距离是点F到直线MN的距离的3倍,求E、F两点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一辆汽车离出发地的距离S(千米)和行驶时间t(小时)之间的函数图象.
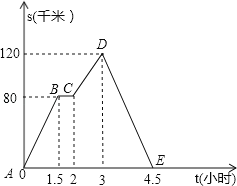
(1)汽车在DE段行驶了 小时;
(2)汽车在BC段停留了 小时;
(3)汽车出发1小时时,离出发地多少千米?
相关试题

