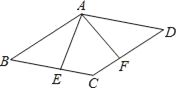
【题目】在菱形ABCD中,AE⊥BC于点E,AF⊥CD于点F,且E、F分别为BC、CD的中点,(如图)则∠EAF等于( )
A. 75°B. 45°C. 60°D. 30°
参考答案:
【答案】C
【解析】
首先连接AC,由四边形ABCD是菱形,AE⊥BC于点E,AF⊥CD于点F,且E、F分别为BC、CD的中点,易得△ABC与△ACD是等边三角形,即可求得∠B=∠D=60°,继而求得∠BAD,∠BAE,∠DAF的度数,则可求得∠EAF的度数.
解:连接AC,
∵AE⊥BC,AF⊥CD,且E、F分别为BC、CD的中点,
∴AB=AC,AD=AC,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
∴AB=BC=AC,AC=CD=AD,
∴∠B=∠D=60°,
∴∠BAE=∠DAF=30°,∠BAD=180°﹣∠B=120°,
∴∠EAF=∠BAD﹣∠BAE﹣∠DAF=60°.
故选:C.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)理数学兴趣小组在探究如何求tan15°的值,经过思考、讨论、交流,得到以下思路:

思路一 如图1,在Rt△ABC中,∠C=90°,∠ABC=30°,延长CB至点D,使BD=BA,连接AD.设AC=1,则BD=BA=2,BC=
 .tanD=tan15°=
.tanD=tan15°= =
= =
=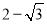 .
.思路二 利用科普书上的和(差)角正切公式:tan(α±β)=
 .假设α=60°,β=45°代入差角正切公式:tan15°=tan(60°﹣45°)=
.假设α=60°,β=45°代入差角正切公式:tan15°=tan(60°﹣45°)=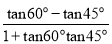 =
= =
= .
.思路三 在顶角为30°的等腰三角形中,作腰上的高也可以…
思路四 …
请解决下列问题(上述思路仅供参考).
(1)类比:求出tan75°的值;
(2)应用:如图2,某电视塔建在一座小山上,山高BC为30米,在地平面上有一点A,测得A,C两点间距离为60米,从A测得电视塔的视角(∠CAD)为45°,求这座电视塔CD的高度;
(3)拓展:如图3,直线
 与双曲线
与双曲线 交于A,B两点,与y轴交于点C,将直线AB绕点C旋转45°后,是否仍与双曲线相交?若能,求出交点P的坐标;若不能,请说明理由.
交于A,B两点,与y轴交于点C,将直线AB绕点C旋转45°后,是否仍与双曲线相交?若能,求出交点P的坐标;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y1=x2+mx+n的图象经过点P(﹣3,1),对称轴是经过(﹣1,0)且平行于y轴的直线.
(1)求m,n的值.
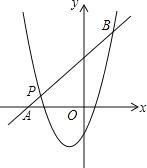
(2)如图,一次函数y2=kx+b的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,点B在点P的右侧,PA:PB=1:5,求一次函数的表达式.
(3)直接写出y1>y2时x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填入相应集合的括号内
+8.5, 0, -3.4, 12, -9,
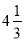 , 3.1415, -1.2,
, 3.1415, -1.2, ,
, 
(1)正数集合 { }
(2)整数集合 { }
(3)负分数集合 { }
(4)非正整数集合{ }
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在数轴上,一动点
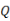 从原点
从原点 出发,沿直线以每秒钟
出发,沿直线以每秒钟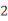 个单位长度的速度来回移动,其移动方式是先向右移动
个单位长度的速度来回移动,其移动方式是先向右移动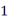 个单位长度,再向左移动
个单位长度,再向左移动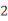 个单位长度,又向右移动
个单位长度,又向右移动 个单位长度,再向左移动
个单位长度,再向左移动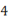 个单位长度,又向右移动
个单位长度,又向右移动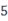 个单位长度…
个单位长度… 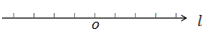
(1)求出
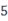 秒钟后动点
秒钟后动点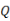 所处的位置;
所处的位置; (2)如果在数轴上还有一个定点
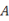 ,且
,且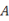 与原点
与原点 相距20个单位长度,问:动点
相距20个单位长度,问:动点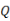 从原点出发,可能与点
从原点出发,可能与点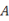 重合吗?若能,则第一次与点
重合吗?若能,则第一次与点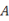 重合需多长时间?若不能,请说明理由.
重合需多长时间?若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在以点O为圆心的两个同心圆中,小圆直径AE的延长线与大圆交于点B,点D在大圆上,BD与小圆相切于点F,AF的延长线与大圆相交于点C,且CE⊥BD.找出图中相等的线段并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】司机小王沿东西大街跑出租车,约定向东为正,向西为负,某天自
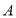 地出发到收工时,行走记录为(单位:千米):+8、-9、+7、-12、+5、-10、+17、-13.
地出发到收工时,行走记录为(单位:千米):+8、-9、+7、-12、+5、-10、+17、-13.回答下列问题:
(1)收工时小王在
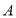 地的哪边?距
地的哪边?距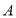 地多少千米?
地多少千米?(2)若每千米耗油0.2升,问从
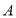 地出发到收工时,共耗油多少升?
地出发到收工时,共耗油多少升?(3)在工作过程中,小王最远离
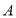 地多远?在
地多远?在 地哪边?
地哪边?
相关试题

